Circuit Problem with Kirchoff's rules (ugh)

[Color_of_Cyan]

Homework Statement

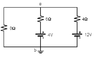
Determine the current in each branch of the circuit shown (here:)
[PLAIN]http://img811.imageshack.us/img811/5084/physicschapter2817.jpg

Homework Equations

Kirchoff's rules, I think is (and I'm probably looking at it wrong):

summation of ΔV around closed loops is 0,

summation of current at any junction is 0(Current) = ΔV / (Resistance), etc

Resistors connected in series = (R1 + R2 +...), etc

The Attempt at a Solution

The red spike lines are resistors.

I am just totally stunned here. This problem got to me to the point of me having to put it here and to draw it in MS paint, and sorry if it looks like an ugly drawing...Anyway the only thing I can do right now is to just simplify the resistors first. Two of em are connected in series so the resistors on the right are simplified to 4 ohms and the ones on the middle line become 6 ohms.

It seems very hard to apply Kirchoff's rules at all and I am not sure how to do apply Kirchoff's rules here. Also I am not sure on what the problem means by "each branch of the circuit. And with the batteries it's even more confusing.

 

[kuruman]

Two pairs of resistors can be simplified (which ones?) To start this problem, you need to draw currents in each branch of the circuit and label them i₁, i₂ etc. Assume a direction; if your assumption is incorrect, when you put in the numbers the currents will be negative. For this circuit you will need two sum of voltages equations and one sum of currents equation.

For future reference, you can draw resistors as skinny rectangles and if you label each as as a number followed by Ω (or "Ohms"), everyone will know them for what they are.

 

[Color_of_Cyan]

Two pairs of resistors can be simplified (which ones?) To start this problem, you need to draw currents in each branch of the circuit and label them i₁, i₂ etc. Assume a direction; if your assumption is incorrect, when you put in the numbers the currents will be negative. For this circuit you will need two sum of voltages equations and one sum of currents equation.

For future reference, you can draw resistors as skinny rectangles and if you label each as as a number followed by Ω (or "Ohms"), everyone will know them for what they are.

I think I may want to know how to make summation of voltages equations and that's probably where I'm having trouble.

I'll get other help from this in the meantime and check back in.

 

[gneill]

Here's your circuit redrawn with the simplifications that you've already described.

There are three branches. I've also labelled two of the nodes as "a" and "b", and we can assume that node "b" represents a common reference point (designated here by the circuit "ground" symbol at node b).

Suppose for the sake of argument that you happened to know the voltage (with respect to node b) at node a. Call it V_a. Can you mark the diagram with currents for each branch and then write KVL equations for those currents for each of them using V_a?