- #1
r_swayze
- 66
- 0
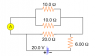
(a) What will the ammeter read? Report this as a positive number. (b) How much power is dissipated by one of the 10.0 Ω resistors?
I am confused about which circuits are in series or parallel wiring. I know the small 10 ohm and 10 ohm loop is parallel, and the 20 ohm to 6 ohm are parallel, correct?
So, the 10 10 ohm loop's equiv resistance = 10*10/(10+10) = 5 ohm
and the 20 6 ohm equiv resistance = 20*6/(20+6) = 4.615 ohm
Now are the two equiv resistances I calculated in series with one another?
I am confused about which circuits are in series or parallel wiring. I know the small 10 ohm and 10 ohm loop is parallel, and the 20 ohm to 6 ohm are parallel, correct?
So, the 10 10 ohm loop's equiv resistance = 10*10/(10+10) = 5 ohm
and the 20 6 ohm equiv resistance = 20*6/(20+6) = 4.615 ohm
Now are the two equiv resistances I calculated in series with one another?