Circular fringes in a Fabry-Perot Interferometer

[Aurora_b]

Homework Statement

Why do we get circular fringes in Fabry-Perot Interferometer experiments?
(This is not really a homework but a doubt I am not able to find an answer to)

Relevant Equations

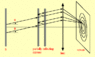
The single beam produces multiple coharent beams in the interferometer, and the emerging set of parallel rays are brought together at some point in the focal plane of the converging lens . The nature of the superposition at P is determined by the path difference between successive parallel beams; taking the refraction index for air as 1, the condition for brightness is

2t cos(theta)=m*L

where t= etalon space
m= integers: 0,1,2.....
L= wavelength

Fabry-Perot Interferometer contains an etalon(an optical cavity created by 2 partially reflective mirrors placed parallel to each other separated by a small distance). When light enters the etalon it gets reflected back and forth between both the mirrors, being partially reflective, every time the beam hits the mirror, a portion of the light is transmitted. So we get a multi beam interference but I am having a difficulty understanding why the interference pattern is circular. In Newton's Rings the shape of the thin film was responsible for the circular fringes but here, the mirrors are parallel the air film is like a cuboid then what is causing the circular fringes?

 

[Charles Link]

The source that you start with for circular fringes is normally diffuse. In this case, each point on the diffuse scatterer becomes a point source from which the pattern emerges that has circular fringes in the far field, as we shall show momentarily: Multiple reflections from the single point source produce a set of images of point sources for this Fabry-Perot case that are equally spaced on the z-axis. Their amplitudes will depend upon the Fresnel coefficients, but in any case, constructive interference for these point sources will occur in the far field at angle $\theta$ when $D \cos{\theta}=m \lambda$, ($\theta$ is polar angle with z-axis), (and note: the path distance to the far field between adjacent sources is an integer number of wavelengths at angles $\theta$ where complete constructive interference occurs), where $D =2 d$ is the spacing between the images. Oftentimes the far field pattern is displayed on a screen in the focal plane of a lens. In any case, each point on the diffuse source produces the same far field circular ring pattern. $\\$ I do think the above theory may apply to the thin film of a bubble as well. The bubble doesn't need to be spherical to get the circular rings. They will occur even in a completely planar geometry. $\\$ Additional comment: The second figure that you have in the OP does not properly explain the circular ring pattern. It is somewhat of a hand-waving explanation. It may be somewhat correct, but hopefully you find my explanation more complete.

 

[Charles Link]

One additional item: In viewing the far field pattern on a screen that is in the focal plane of a lens, this will bring the interference pattern to a focus, where parallel rays at a given angle come to focus at a given point in the focal plane. It will not bring the diffuse source to a focus, because the location (m, not to be confused with the integer m above) of the screen for that to occur is such that $\frac{1}{b}+\frac{1}{m}=\frac{1}{f}$