- #1
ColoradoGrrrl
- 1
- 1
- Homework Statement
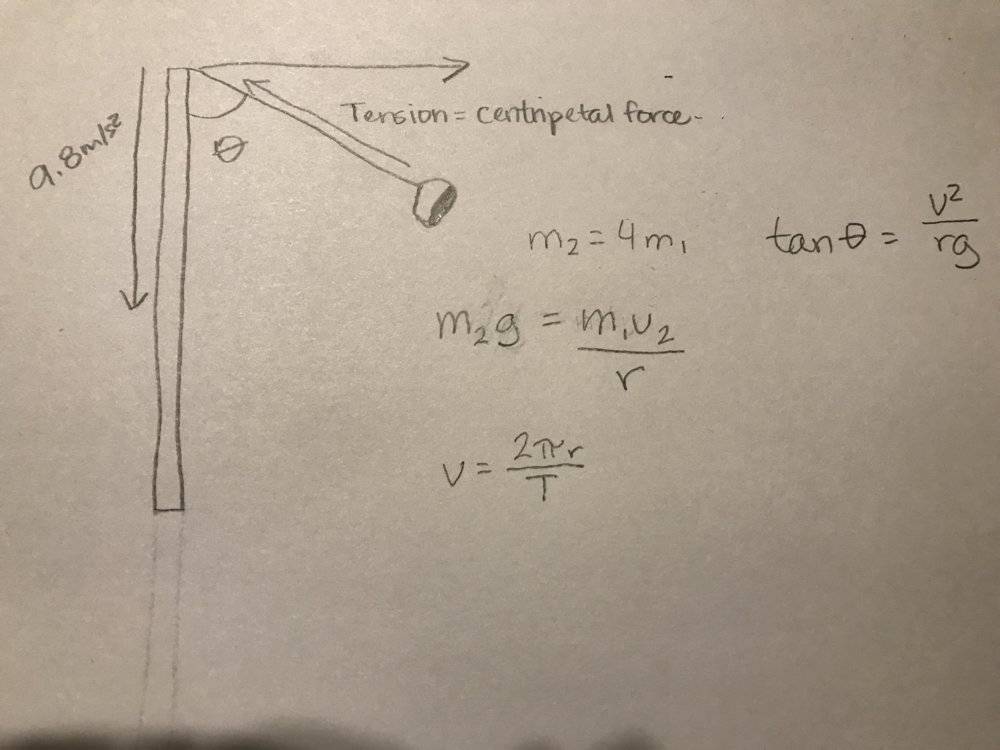
- 1. Draw a free body diagram and solve for the centripetal acceleration in terms of θ and g for one person riding on the amusement park ride in Figure 3. A free-body diagram will show that the centripetal force on the rotating mass m1, is provided by the weight of the hanging mass m2. Since those forces must be equal, we can write the equation: m2g = m1v2/r where v is the velocity of m1, and r is the radius of its circular path. Since the magnitude of the velocity is the average distance divided by the average time, we can write the velocity = the circumference / the period, or v = 2πr/T where the period T is the time to complete one revolution. Assume m2 = 4m1. Write an expression for the period in terms of r and g. You should find the mass terms will drop out.
- Relevant Equations
- m2=4m1
m2g=m1v2/r
v=2piR
I'm not sure if I'm doing this right as far as coming up with the equation they are asking for. I feel the question is poorly worded and the formatting makes their equation notation difficult to understand. Any insight would be very helpful. This is my work so far: