- #1
vinci
- 12
- 4
[Moderator's Note: Thread moved from forum General Physics hence no formatting template]
I am trying to study Circular Motion for my exams and I'm kind of unsure about one question. The question asks what's keeping the truck in circular motion. It has to be gravity I know, but gravity being directed towards the center, shouldn't that just result in the truck falling? What keeps it INTACT to the track? I am giong to quote the actual question now.
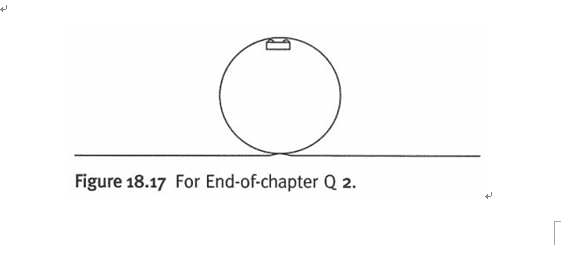
"Figure 18.17 shows part of the track of a roller-coaster ride in which a truck loops the loop. When the truck is at the position shown there is no reaction force between the wheels of the truck and the track. The diameter of the loop in the track is 8.0 m.
a) Explain what provides the centripetal force to keep the truck moving in a circle.
b) Given that the acceleration due to gravity g is 9.8 m s-2, calculate the speed of the truck.
 "
"
I am trying to study Circular Motion for my exams and I'm kind of unsure about one question. The question asks what's keeping the truck in circular motion. It has to be gravity I know, but gravity being directed towards the center, shouldn't that just result in the truck falling? What keeps it INTACT to the track? I am giong to quote the actual question now.
"Figure 18.17 shows part of the track of a roller-coaster ride in which a truck loops the loop. When the truck is at the position shown there is no reaction force between the wheels of the truck and the track. The diameter of the loop in the track is 8.0 m.
a) Explain what provides the centripetal force to keep the truck moving in a circle.
b) Given that the acceleration due to gravity g is 9.8 m s-2, calculate the speed of the truck.