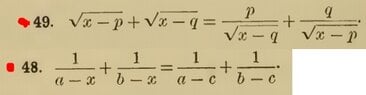Clarifying some rules on solving quadratic equation

[NotaMathPerson]

View attachment 5675
Hello! I just want to clarify something about the rules on solving quadratic eqns.

I have already solved both problems but in the process of my solution some questions arise.

For example in the part of my soltution in problem 48 I have this

$(x-c)\left(\frac{a^2+b^2-ac-bc+x(2c-a-b)}{x^2-ax-bx+ab}\right)=0$

Multiplying both sides by $(x^2-ax-bx+ab)$ I get two unqueal roots. I got the correct ansswer for this one

But when I divide both sides by $(x-c)$ I only get one root.

And also for 49

In the part of my solution I have

$x\left(\frac{1}{\sqrt{x-p}}+\frac{1}{\sqrt{x-q}}\right)=(p+q)\left(\frac{1}{\sqrt{x-q}}+\frac{1}{\sqrt{x-p}}\right)$

Dividing both sides by $\left(\frac{1}{\sqrt{x-q}}+\frac{1}{\sqrt{x-p}}\right)$

I get x=p+q which is the correct answer

Now my questions are the following

In prob 48, when I divide both sides of the equation by $x-c$ I end up having one root
In prob 49 when I divide both sides by $\left(\frac{1}{\sqrt{x-q}}+\frac{1}{\sqrt{x-p}}\right)$ I end up with two equal roots

I divided both sides of the equations for both problems by a factor which contain x and I ended up having one root for prob 48 and two equal roots for 49. Can you tell me why is it the case.

I know the reason why I get a single root for prob 48. It is because of the fact that x=c is a solution. But what I am having trouble with is the fact that I used the same process(dividing both sides by a factor containing x) for prob 49 and still end up with two equal roots. Please explain it. Thanks

 

[soroban]

$$49.\;\sqrt{x-p} + \sqrt{x-q} \;=\;\frac{p}{\sqrt{x-q}} + \frac{q}{\sqrt{x-p}}$$

Multiply both sides by $$\sqrt{x-p}\sqrt{x-q}:$$

. . 0. . $$(x-p)\sqrt{x-q} + (x-q)\sqrt{x-p} \;=\;p\sqrt{x-p} + q\sqrt{x-q}$$

. . .. . $$(x-p)\sqrt{x-q} - q\sqrt{x-q} + (x-q)\sqrt{x-p} - p\sqrt{x-p} \;=\;0$$

$$\text{Factor: }\;(x-p-q)\sqrt{x-q} + (x-p-q)\sqrt{x-p} \;=\;0$$

$$\text{Factor: }\;(x-p-q)(\sqrt{x-q} + \sqrt{x-p}) \;=\;0$$

$$\text{Therefore: }\;x-p-q\:=\:0 \quad\Rightarrow\quad x \:=\: p+q$$

 

[NotaMathPerson]

Arent we suppose to get two roots for this problem? Since we have a quadratic equation. Anyone please explain this for me.

 

[squidsk]

Arent we suppose to get two roots for this problem? Since we have a quadratic equation. Anyone please explain this for me.

There's no guarantee that a quadratic equation has two roots. Further from the last equation the second root would be derived from:

$$\sqrt{x - q} + \sqrt{x - p} = 0$$

Which if you aren't dealing with complex numbers, which wasn't given in your original question, only has one possibility of being 0 which is [math]x = p = q[/math]. Can you see why?

As for question 48, the reason you only get one root when dividing out the [math]x - c[/math] is that you've divided out term that gets you one of the roots.

 

[NotaMathPerson]

There's no guarantee that a quadratic equation has two roots. Further from the last equation the second root would be derived from:

$$\sqrt{x - q} + \sqrt{x - p} = 0$$

Which if you aren't dealing with complex numbers, which wasn't given in your original question, only has one possibility of being 0 which is [math]x = p = q[/math]. Can you see why?

As for question 48, the reason you only get one root when dividing out the [math]x - c[/math] is that you've divided out term that gets you one of the roots.

Do you mean that the other solution is x=p=q?
Anyone? Hello?