Classical Mechanics: Fictitious Forces: Centrifugal, Coriolis, Transverse, etc.

[alimerzairan]

Homework Statement

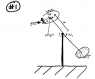
Figure is attached.

In an amusement park ride called the hammer a large beam rotates in a ver- tical plane about a central pivot (see figure). Cages are attached to the end of the beam; these rotate independently. The riders are strapped to the walls of the cages. The center of the cage is a distance a from the central pivot and the rider is a distance b from the secondary pivot. During most of the ride the angular frequency ω1 of the central pivot is constant but the angular frequency of the cage ω2 is variable. Choose the end of the beam as your origin and allow the coordinate system to rotate with the cage. Give the name, magnitude, and direction of all fictitious accelerations experienced by the rider. Assume ω1 is constant (since it is for most of the ride).

Homework Equations

m \ddot{\vec{r}} = \vec{F} - m \vec{A} - m \dot{\vec{\Omega}} \times \vec{r} - 2m \vec{\Omega} \times \dot{\vec{r}} - m \vec{\Omega} \times (\vec{\Omega} \times \vec{r})
Only this equation.

The Attempt at a Solution

I am a bit confused on the fictitious forces (meaning which ones there are).

I set the coordinate system to the origin of the cage. Therefore, the \vec{A} will be nonzero and will be based on the centripetal acceleration of the cage. For the rider, he will experience a centrifugal force based on the way we set up our coordinate system and reference frame. There will also be a transverse or azimuthal force from (- m \dot{\vec{\Omega}} \times \vec{r}) the variable angular velocity of the cage.

Now, my two questions are: do we have a Coriolis Force despite that the rider is constrained to move around the origin of radius b?; are the fictitious forces stated and my logic correct?

 

[alimerzairan]

Anyone? Is the question confusing or do you not know what I am asking? My main concern is if there does exist a Coriolis Force and why would there be one.

 

[macrsp]

This is a way late response to this thread - but for the sake of anyone else that finds this thread to be interesting.

Consider if you have any \dot{\vec{r}} in the reference frame that is centered on the main pivot point and with the horizontal axis fixed to the large beam if {\vec{r}} is the distance between the rider and the central pivot.

If you do have \dot{\vec{r}}, then the coriolis term shouldn't be zero - but if you don't have \dot{\vec{r}}, then the term would be zero.

Note that this won't give you an answer for the direction of the force, as it is from the frame fixed to the beam, not the riders frame. Fictous forces are fun because they depend on the reference frame.