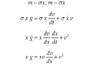HAMJOOP
- 31
- 0
From (Marion 5th ed. Problem 9-15)
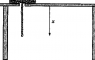
A smooth rope is placed above a hole in a table. One end of the rope falls through the hole at t = 0, pulling steadily on the remainder of the rope. Find the velocity and acceleration of the rope as a function of the distance to the end of the rope x.
Ignore all friction. The total length of the rope is L.
I attempt to solve it by lagrangian L = T - U
T = 1/2 (λx) v^2
U = -(λx)g(x/2)
where λ is mass density
But someone said it is not correct. He claimed that if T depends on generalized coordinate explicitly(in this case x), then it violates Newton's Second Law.
So, lagrangian mechanics cannot be used in open system ?
Marion's Solution
F = dp/dt = m(dv/dt) + v(dm/dt) (see Fig)
I learned that we cannot differentiate m (i.e. dm/dt) if the system is open.
So, which one is correct ??
Can anyone explain to me in detail ?
A smooth rope is placed above a hole in a table. One end of the rope falls through the hole at t = 0, pulling steadily on the remainder of the rope. Find the velocity and acceleration of the rope as a function of the distance to the end of the rope x.
Ignore all friction. The total length of the rope is L.
I attempt to solve it by lagrangian L = T - U
T = 1/2 (λx) v^2
U = -(λx)g(x/2)
where λ is mass density
But someone said it is not correct. He claimed that if T depends on generalized coordinate explicitly(in this case x), then it violates Newton's Second Law.
So, lagrangian mechanics cannot be used in open system ?
Marion's Solution
F = dp/dt = m(dv/dt) + v(dm/dt) (see Fig)
I learned that we cannot differentiate m (i.e. dm/dt) if the system is open.
So, which one is correct ??
Can anyone explain to me in detail ?