Classical Mechanics - Moving Object in 3D space

[TanGeriN]

Homework Statement

Hello, i have the following task, which should actually not be too hard, but for for some reason i cannot figure out the answer.

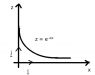
Consider an Object with 1 kg mass in 3D space with coordinates $\vec r = [x(t), y(t), z(t)]$. Like Shown in the attachment, $z:= e^{ax}$ and furthermore y = 0 (always).

a) Calculate the potential energy and the kinetic energy at x = 0 and velocity $\vec v(t) = 0$

b) Calculate the potential energy and the kinetic energy at $x = \eta$ and$z = e^{a\eta}$. $\eta$ is some real number.

c) Calculate the velocity $\vec v(t)$ and the direction of the object at $x = \eta$

Homework Equations

I know the following equations for kinetic and potetial energy:

Potential energy: $V(\vec r) = m*h*g$, where hight h might be z ...
Kinetic energy: $T(t) = \frac{1}{2} m v^2$

The Attempt at a Solution

At first i wanted to use these equations above, but the problem is, that there is actually no force field given in this task ... also gravity is not mentioned explicitly. Is it even possible to solve this task without having a force? Maybe, I'm using the wrong equations. I also thought of $V(\vec r) = \int \vec F(\vec r)$ for the potential.
It might be necessary (and reasonable) to assume gravity as the force field ...


I hope that somebody can help me.

 

[BvU]

Strange. 3D space goes very far. Makes a difference if you are on Earth or way beyond Alpha Centauri.

your z is $e^{-ax}$ in the attachment, by the way. I don't understand what you mean with z:=

 

[AlephZero]

If it is moving along a curve, there must be some force acting on it to accelerate it. What do you know about constraint forces and changes in PE and KE?

The question testing if you understand the basics ideas of mechanics, not if you can plug and chug algebra formulas.