Classical Mechanics - Pulleys System

[TomAlso]

Homework Statement

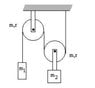
Consider the pulleys system in the picture. Assume both pulleys are frictionless. Assume the rope is massless and inextensible. Find the acceleration of the mass m_2

Homework Equations

The Attempt at a Solution

I have solved the same problem with massless pulleys and I fail to see if their radii should be involved at all in the final result. So first notice that the acceleration of the mass m_2 is half of the acceleration of the mass m_1. On m_1 we have:

m_1 g - T = m_1 a

On m_2 we have:

2T - (m+m_2)g = (m+m_2) \cdot \frac{a}{2}

which solves for

a = \frac{2*(m + m_2 - 2 m_1)}{4 m_1 + m + m_2}

Anyone can offer any advice? In particular, how am I supposed to include the radius of the pulleys and the pulley that does not figure in the equation? Thank you!

 

[ninjadrummer8]

can you post the picture a different way? I can't see the attachment

 

[TomAlso]

The picture is just like http://img84.imageshack.us/i/carrucoleesameot5.jpg/" . Both pulleys have mass m and radius r. The mass labeled A is m_1 and B is m_2.

It says my attachment is pending approval, maybe that is the problem.

 

[Doc Al]

Anyone can offer any advice? In particular, how am I supposed to include the radius of the pulleys and the pulley that does not figure in the equation?

(1) Since the pulleys have mass, you cannot assume that the tension in the rope is the same throughout. Treat each rope segment as having a different tension; Label the tensions T₁, T₂, and T₃.
(2) Don't ignore the rotational inertia of the pulleys. I presume that you can model the pulleys as uniform disks. (You'll need to analyze both pulleys.)