Clausius' Theorem: Solving the Mystery of T ∑(dQi/Ti) =< 0

[Pouyan]

Homework Statement

Derive the Clausius' theorem

Relevant Equations

Qh/Ql= Th/Tl
ΔW= ΣdQi

I see this in my book but there is something I don't get!
If we consider a Carnot cycle where heat Qh enters and heat Ql leaves,
We know Qh/Ql=Th/Tl
And we define ΔQ_rev then :

∑(ΔQ_rev/T) = (Qh/Th) - (Ql/Tl) =0
I insert an image:

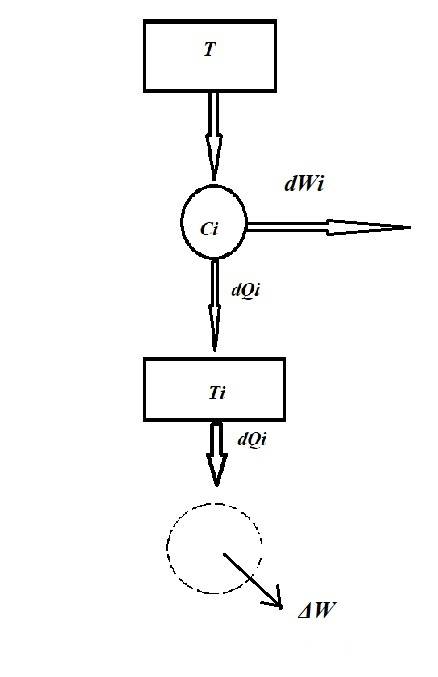
Which shows the heat dQi entering the reservoir at Ti from a reservoir at temperature T via a Carnot (Ci).
We know:

heat to reservoir at Ti / Ti = heat from the reservoir at T/ T
So : dQi/Ti = (dQi+dWi)/T
and rearranging:
dWi=dQi((T/Ti) -1)

The system in the image seems to convert heat to work but it cannot convert 100% of heat to work according to Kelvin's statement of the second law and hence we must insist that this is not the case. Hence:

Total work produced per cycle = ΔW + ∑(dWi) =< 0

But there is something I don't understand!

ΔW = ∑(dQi)
and dWi=dQi((T/Ti) -1)

So the total work produced per cycle = T ∑(dQi/Ti)

But why we say that this is less or equal than zero ?
T ∑(dQi/Ti) =< 0

T > 0.
Ti must be more than zero of course (Ti > 0)
How can we say that dQi =< 0 ?
Is that because it leaves from the reservoir with lower temperature ?

 

[Chestermiller]

$$W=Q_H\left(1-\frac{T_i}{T_H}\right)$$
$$0<T_i<T_H$$

 

[Pouyan]

$$W=Q_H\left(1-\frac{T_i}{T_H}\right)$$
$$0<T_i<T_H$$

Would you explain please?

 

[Chestermiller]

Would you explain please?

This just follows from the equations you wrote. What part don’t you understand?

 

[Pouyan]

This just follows from the equations you wrote. What part don’t you understand?

T ∑(dQi/Ti) =< 0

Is that correct to think dQi <=0 because it leaves the reservoir?

 

[Chestermiller]

T ∑(dQi/Ti) =< 0

Is that correct to think dQi <=0 because it leaves the reservoir?

In a cycle, the change in entropy of the working fluid is zero, and the Q's represent heat flows to the working fluid. So, if one of the Q's is negative, it means that the heat is flowing from the working fluid to a reservoir.