CGandC
- 326
- 34
Homework Statement
Hello,
I have a general question regarding to coefficient matching when spanning some function, say , f(x) as a linear combination of some other basis functions belonging to real Hilbert space.
Homework Equations
- Knowledge of power series, polynomials, Legenedre polynomials, Spherical harmonics..
The Attempt at a Solution
Say I express f(x) as a power series, and f(x) = 1+2x+3x^2 , so, I can match the coefficients as in the following picture:
( no problem there, since the series is a polynomial)
Ok..but what If I now have some function g(x) and I express it as Legendre series (in the x domain: -1 to 1 ) , and I know that
My question is , can I apply coefficient matching here? ( as in the next picture: )
Also, consider the next case:
suppose I have :
then, matching coefficients I get:
Eventually, I get a contradiction , on the one hand : A=2 , on the other hand A=3 , so my understanding of coefficient matching in this part is clearly wrong ( because it aint a series representing polynomials? )... why?
Note:
I was taught that coefficient matching works in polynomials and since power series is a polynomial, but Legendre series and the last series is different... yet, I was not told that coefficient matching does not work in other cases, that makes me troubled as I'm unsure if coefficient matching applies only to polynomials.
Much thanks in advance for helpers.
Attachments
-
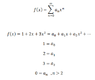 upload_2018-1-8_21-52-57.png2.4 KB · Views: 598
upload_2018-1-8_21-52-57.png2.4 KB · Views: 598 -
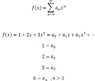 upload_2018-1-8_21-53-11.png2.3 KB · Views: 452
upload_2018-1-8_21-53-11.png2.3 KB · Views: 452 -
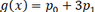 upload_2018-1-8_21-55-3.png626 bytes · Views: 572
upload_2018-1-8_21-55-3.png626 bytes · Views: 572 -
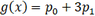 upload_2018-1-8_21-55-17.png651 bytes · Views: 425
upload_2018-1-8_21-55-17.png651 bytes · Views: 425 -
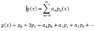 upload_2018-1-8_21-56-52.png1.6 KB · Views: 558
upload_2018-1-8_21-56-52.png1.6 KB · Views: 558 -
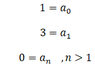 upload_2018-1-8_21-58-9.png779 bytes · Views: 612
upload_2018-1-8_21-58-9.png779 bytes · Views: 612 -
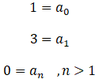 upload_2018-1-8_21-58-19.png773 bytes · Views: 438
upload_2018-1-8_21-58-19.png773 bytes · Views: 438 -
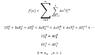 upload_2018-1-8_22-7-54.png2.6 KB · Views: 584
upload_2018-1-8_22-7-54.png2.6 KB · Views: 584 -
 upload_2018-1-8_22-9-53.png791 bytes · Views: 583
upload_2018-1-8_22-9-53.png791 bytes · Views: 583 -
 upload_2018-1-8_22-9-55.png791 bytes · Views: 577
upload_2018-1-8_22-9-55.png791 bytes · Views: 577 -
 upload_2018-1-8_22-10-7.png791 bytes · Views: 408
upload_2018-1-8_22-10-7.png791 bytes · Views: 408 -
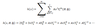 upload_2018-1-8_22-11-2.png2.5 KB · Views: 431
upload_2018-1-8_22-11-2.png2.5 KB · Views: 431 -
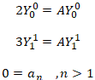 upload_2018-1-8_22-11-32.png914 bytes · Views: 405
upload_2018-1-8_22-11-32.png914 bytes · Views: 405 -
 upload_2018-1-8_22-22-25.png1.3 KB · Views: 610
upload_2018-1-8_22-22-25.png1.3 KB · Views: 610 -
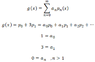 upload_2018-1-8_22-23-24.png1.9 KB · Views: 603
upload_2018-1-8_22-23-24.png1.9 KB · Views: 603 -
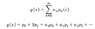 upload_2018-1-8_22-24-16.png1.5 KB · Views: 433
upload_2018-1-8_22-24-16.png1.5 KB · Views: 433