CarlosMarti12
- 7
- 0
Hello everyone!
I have calculated the velocities required for an orbiting body to follow a circular, parabolic, and hyperbolic trajectory around another massive body, which are the following:
v_{circular} = \sqrt{\frac{\mu}{r}} = \sqrt{\frac{GM}{r}}
v_{parabolic} = \sqrt{\frac{2\mu}{r}} = \sqrt{\frac{2GM}{r}} = v_{circular} \times \sqrt{2}
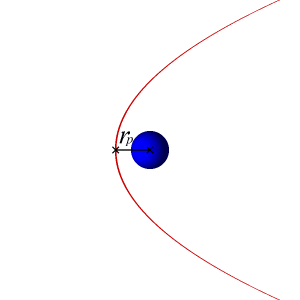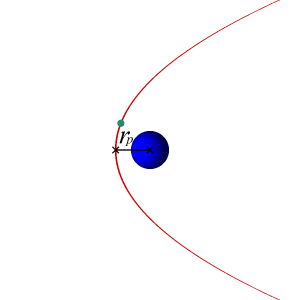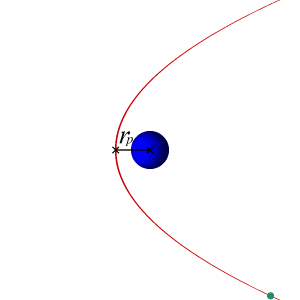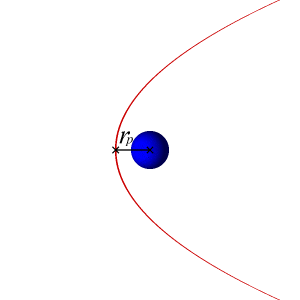
v_{hyperbolic} > v_{parabolic}
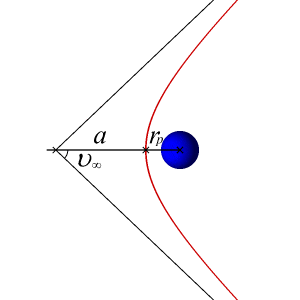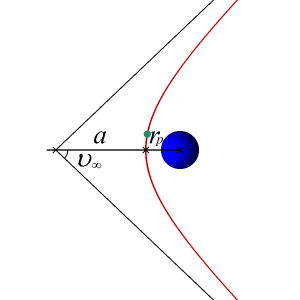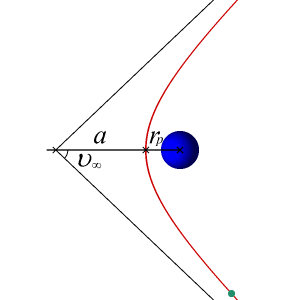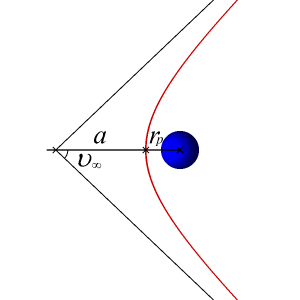
An article about the different orbital trajectories can be found here: http://en.wikibooks.org/wiki/Astrodynamics/Orbit_Basics
I am now trying to calculate the velocity required for an orbiting body to follow a trajectory that leads to a collision with the massive body. Of course, we would now have to factor in the radius of the objects, since we could previously consider them point masses to calculate their trajectories. But bodies have extension (in this case, spherical would be sufficient), and their extension must be taken into account to calculate collisions. So we must add the radius of the objects, r_{body} into the equation... somehow.
I have failed to find a way to do this based on the parameters shown above (gravitational constant, mass, distance, radii), though I highly expect I'm missing something (perhaps something obvious). Does anyone know how to calculate the velocity required for an orbiting body to enter a crash course trajectory with a massive body?
Any help, as always, would be greatly appreciated!
I have calculated the velocities required for an orbiting body to follow a circular, parabolic, and hyperbolic trajectory around another massive body, which are the following:
v_{circular} = \sqrt{\frac{\mu}{r}} = \sqrt{\frac{GM}{r}}
v_{parabolic} = \sqrt{\frac{2\mu}{r}} = \sqrt{\frac{2GM}{r}} = v_{circular} \times \sqrt{2}
v_{hyperbolic} > v_{parabolic}
An article about the different orbital trajectories can be found here: http://en.wikibooks.org/wiki/Astrodynamics/Orbit_Basics
I am now trying to calculate the velocity required for an orbiting body to follow a trajectory that leads to a collision with the massive body. Of course, we would now have to factor in the radius of the objects, since we could previously consider them point masses to calculate their trajectories. But bodies have extension (in this case, spherical would be sufficient), and their extension must be taken into account to calculate collisions. So we must add the radius of the objects, r_{body} into the equation... somehow.
I have failed to find a way to do this based on the parameters shown above (gravitational constant, mass, distance, radii), though I highly expect I'm missing something (perhaps something obvious). Does anyone know how to calculate the velocity required for an orbiting body to enter a crash course trajectory with a massive body?
Any help, as always, would be greatly appreciated!