Trajectory collision calculation

[pejsek]

TL;DR Summary

Calculate α so that the red and blue objects meet using the given parameters

Hello,

I ask you for your aid in the solution of the following problem. Please see the attached illustration.

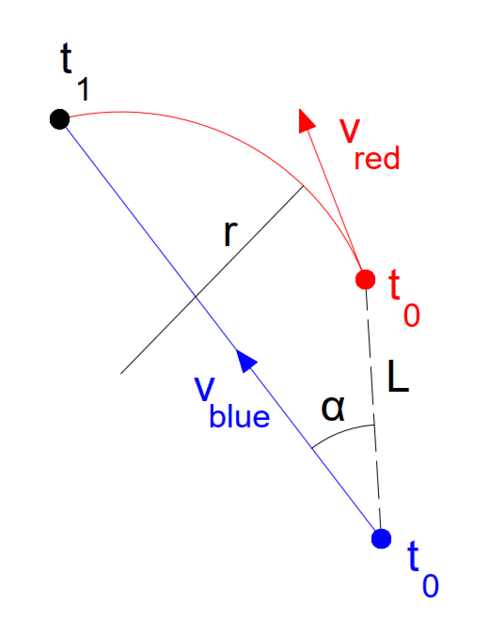
Two objects (red and blue) are moving in the vicinity of each other. The red object is moving along a closed circle and the blue object is moving along a line. Our objective is to make the two objects collide. We cannot touch the red object, however, we can change the direction of the movement of the blue object by changing the angle α. The goal is to calculate the angle α so that the two objects meet.

Here is what is known:
L ... distance between the two objects at time = 0
r ... radius of the trajectory of the red object
v_red ... magnitude of the tangential velocity of the red object
v_blue ... magnitude of the velocity of the blue object

Magnitudes of both velocities are constant (there is no acceleration except for the centripetal acceleration of the red object).

This problem comes from my idea of calculating the angle at which fighter planes have to fire their guns when shooting down an enemy aircraft in a turn.

Thank you very much indeed for your help,
pejsek

 

[Mister T]

What's your approach to solving this problem? Do you have any ideas?

 

[pejsek]

This is as far as I have got. I am either missing one more equation or the whole approach is wrong.

 

[Filip Larsen]

Since A and B eventually has to be at the same position at the same time (a so-called kinematic intercept problem), perhaps you can formulate your problem in a way that facilitates a solution in that way?

 

[A.T.]

This problem comes from my idea of calculating the angle at which fighter planes have to fire their guns when shooting down an enemy aircraft in a turn.

Sounds like a common problem. Did you search the web for a solution?

Here is some discussion of it I found:
https://gamedev.stackexchange.com/questions/75015/how-can-i-intercept-object-with-a-circular-motion
https://physics.stackexchange.com/q...-move-to-intercept-another-object-moving-alon

 

[berkeman]

This is as far as I have got. I am either missing one more equation or the whole approach is wrong.

View attachment 330573

Wow, that is mostly illegible for me. Please review the LaTeX Guide link at the lower left of the Edit box to learn how to post math equations here at PF. I will send you a separate Private Message (PM) with more information on using LaTeX.

 

[Juanda]

Have you tried solving an easier version of the problem first? For example, replacing the circular path with a straight path.

When facing something that initially looks too challenging it is often useful trying to solve similar easier things. It helps to build intuition and practice that can then be used in the original problem.
With the straight lines the system of equations will be significanlly easier and the solution will be unique since two straight lines only cross at one point. With the circular path the system of equations necessary will be more tedious to solve and you'll get more possible solutions since, normally, the straight line will be able to intersect the circle twice.