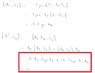Commutation relation using Levi-Civita symbol

[davon806]

Homework Statement

Hi,I have got a question as follow:
Compute the commutation relations of the position operator R and the angular momentum L.Deduce the commutation relations of R^2 with the angular momentum L

Homework Equations

The Attempt at a Solution

In fact I have got the solutions to this problem.I am having trouble for the 2nd part of the question.
In the red box of the image,why did the terms cancel out?Since position vector is commutative I expect they should add up?

Thanks!

 

[TSny]

You are correct that the two terms in the first line of the red box are equal. Try to show that each term separately equals zero.

 

[davon806]

You are correct that the two terms in the first line of the red box are equal. Try to show that each term separately equals zero.

But if k =/= l ,then the first term becomes i(h bar) (x1x2 + x2x1+x3x2+x2x3 + x3x1 + x1x3)?

 

[TSny]

Note that $j$ is some fixed value.

Take the specific case where $j = 1$. Then what does the first term become when you sum over $k$ and $l$?

 

[davon806]

Note that $j$ is some fixed value.

Take the specific case where $j = 1$. Then what does the first term become when you sum over $k$ and $l$?

So if j =1,then we can either have k = 2,l = 3 or k = 3,l = 2.Hence the nonzero possibility of epsilon becomes e(132) or e(123)
i(h bar)(x2x3 - x3x2) =0 ?

 

[TSny]

Yes, that's correct.