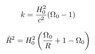Comoving distance, causality volume and entropy

[Xkcd]

Hello everyone !

I try to find the expression of the time derivative of the entropy for the CMB (photon gas) but I am stuck with the calculations.

We are in the matter-domination area and at the present time (Ro=1). No radiation and no vacuum, only the curvature. The different equations are:

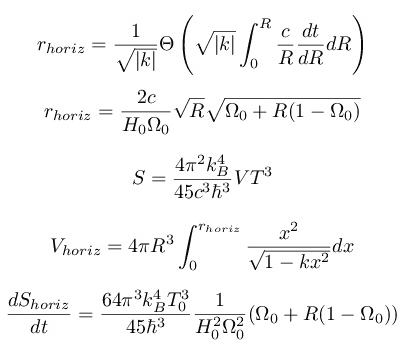
The problem is that the equations are resolved regardless of the spatial curvature of the universe. For the comoving distance I used :

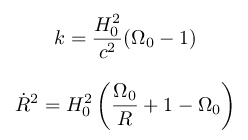
But I cannot find the same result. I have

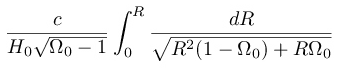
If I use a calculator I have an equation with logarithm and I do not find the previous result andI cannot find where is my mistake.

And I have a similar problem with the integral for the volume. With a calculator I have a monster with Arcsin and I cannot find the final expression for the entropy.

If someone could help me with the different steps for the two integrals so that I can find the expression for the derivative of the entropy.

Thank you !

 

[kimbyd]

Why are you using equations for a horizon? There is no cosmological horizon in a matter-dominated universe.

For the time derivative of the entropy of the CMB photon gas, you just need the entropy of a photon gas (which is a function of its temperature), and how that photon gas evolves with time (which is pretty simple in a matter-dominated universe).