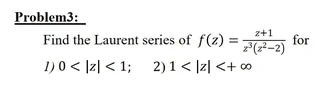Homework Help Overview
The discussion revolves around finding the Laurent series for the function \( f(z) = \frac{z+1}{z^3(z^2-2)} \) in specified domains. Participants are examining the validity of the problem as presented, particularly focusing on the convergence regions of the series expansions.
Discussion Character
Approaches and Questions Raised
- Some participants question the validity of the problem statement, suggesting alternative functions and domains that would make more sense. Others discuss the implications of poles in relation to the convergence of the Laurent series.
Discussion Status
The discussion is ongoing, with participants exploring different interpretations of the problem. Some have provided guidance on using partial fraction decomposition and series expansions, while others emphasize the need for clarification regarding the function and its intended domain.
Contextual Notes
There are concerns about the convergence of the series at specific points, particularly at \( z = \sqrt{2} \), which is identified as a pole of the function. Participants are also discussing the implications of the teacher's instructions and the need for accurate domain specifications.