peroAlex
- 35
- 4
Hello!
Recently I was going through some old exams and upon encountering this problem (which seemed pretty easy) I got stuck. Exams at my university are composed of individual tasks, each having three subquestions with four plausible answers respectively. Solution sheet gives results only, so there’s no way for me to check where my attempt at solution went wrong. I ask members of this forum for help, maybe someone will see where I made a mistake. Your help is very appreciated, so thank you in advance.
----------------------------------------------------------
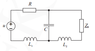
Task gives a circuit with following data: ## u(t) = 60 \cos{\omega t} ##, ## R = 10 \Omega ##, ##X_C = -3j \Omega ##, ## X_{L1} = 10j \Omega ## and ##X_{L2} = 20j \Omega ##.
First question asks for absolute value of impedance ##|Z_b|##.
Second question asks for maximum power dissipated on the load ##Z_b##.
Third question asks for current amplitude through load ##Z_b##.
My university provides a formula sheet, so for this question I believe only ##P_max = \frac{|U_{Th}|^2}{8 \cdot R_{Th}} ## is relevant here. If anyone thinks I’m missing some equation, please mention it in reply.
So first of all, computing Thevenin resistance (first question) was pretty simple, just use $$ R_{Th} = jX_{L2} + \frac{ (R+jX_{L1}) (jX_C) }{(R+jX_{L1}) + (jX_C)} = 0.604 + 16.577j \Omega$$ and for the final touch compute absolute value of complex number ## |R_{Th}| = 16.588 \Omega ##. Solution sheet agrees with me.
Now for second and third question I’ve been banging my head for the past 6 hours. Correct result should be that power dissipated on the load is ##P_{max} = 45 W ## and that current amplitude through the load should be ##I_0 = 12.2 A##. My very first attempt was finding current in each loop.
Solving system of equations ## I_1 (R + jX_{L1} + jX_C) + I_2 (jX_C) = -60 ## and ##I_2 (16.588 + jX_{L2} + jX_C) + I_1(X_C) = 0 ## yields two complex currents ##I_1 = -4.088 + 2.680i ## and ##I_2 = -0.606 – 0.118i ##. So using second current (in absolute) times previously computed resistance yields ##U_Th = 10.241 U## and ##P_{max} = 0.790 W##.
I don’t know how to solve this task, been through videos on YouTube, visited sites like Hyper Physics (which helped me compute Thevenin impedance. Could someone please help me? At least a hint or by pointing me in the right direction.
----------------------------------------------------------
By the way, I really hope you’re having a lovely Monday!
Recently I was going through some old exams and upon encountering this problem (which seemed pretty easy) I got stuck. Exams at my university are composed of individual tasks, each having three subquestions with four plausible answers respectively. Solution sheet gives results only, so there’s no way for me to check where my attempt at solution went wrong. I ask members of this forum for help, maybe someone will see where I made a mistake. Your help is very appreciated, so thank you in advance.
----------------------------------------------------------
Homework Statement
Task gives a circuit with following data: ## u(t) = 60 \cos{\omega t} ##, ## R = 10 \Omega ##, ##X_C = -3j \Omega ##, ## X_{L1} = 10j \Omega ## and ##X_{L2} = 20j \Omega ##.
First question asks for absolute value of impedance ##|Z_b|##.
Second question asks for maximum power dissipated on the load ##Z_b##.
Third question asks for current amplitude through load ##Z_b##.
Homework Equations
My university provides a formula sheet, so for this question I believe only ##P_max = \frac{|U_{Th}|^2}{8 \cdot R_{Th}} ## is relevant here. If anyone thinks I’m missing some equation, please mention it in reply.
The Attempt at a Solution
So first of all, computing Thevenin resistance (first question) was pretty simple, just use $$ R_{Th} = jX_{L2} + \frac{ (R+jX_{L1}) (jX_C) }{(R+jX_{L1}) + (jX_C)} = 0.604 + 16.577j \Omega$$ and for the final touch compute absolute value of complex number ## |R_{Th}| = 16.588 \Omega ##. Solution sheet agrees with me.
Now for second and third question I’ve been banging my head for the past 6 hours. Correct result should be that power dissipated on the load is ##P_{max} = 45 W ## and that current amplitude through the load should be ##I_0 = 12.2 A##. My very first attempt was finding current in each loop.
Solving system of equations ## I_1 (R + jX_{L1} + jX_C) + I_2 (jX_C) = -60 ## and ##I_2 (16.588 + jX_{L2} + jX_C) + I_1(X_C) = 0 ## yields two complex currents ##I_1 = -4.088 + 2.680i ## and ##I_2 = -0.606 – 0.118i ##. So using second current (in absolute) times previously computed resistance yields ##U_Th = 10.241 U## and ##P_{max} = 0.790 W##.
I don’t know how to solve this task, been through videos on YouTube, visited sites like Hyper Physics (which helped me compute Thevenin impedance. Could someone please help me? At least a hint or by pointing me in the right direction.
----------------------------------------------------------
By the way, I really hope you’re having a lovely Monday!