Concept question: Angular momentum

[jegues]

Homework Statement

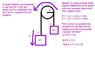
A pulley with radius R and rotational inertia I is free to rotate on a horizontal fixed axis through its center. A massless string passes over the pulley. A block of mass m1 is attached to one end and a block of mass m2 is attached to the other. At one time the block with mass m1 is moving downward with speed v. If the string does not slip on the pulley, the magnitude of the total angular momentum, about the pulley centre, of the blocks and the pulley, considered as a system is given by:

Homework Equations

L = l1 + l2 + l3...

l = rxp
l = Iw

The Attempt at a Solution

In my diagram.

I may have answered my question by rewriting the question out, but I'd like to double check.

Is the v on m2 not negative because the question says the magnitude?

Thanks again,

 

[kuruman]

L = mr x v. If for one mass you take r positive and v also positive, then for the other mass both r and v are negative which means that the angular momentum of the other mass is also positive.

 

[jegues]

How can the radius for the other mass be negative?

 

[kuruman]

Note that I put r in bold. That means that it is a vector. If you draw the two r's, you will see that they point in opposite directions. Angular momentum is also a vector, so direction matters when you add two angular momenta together.