- #1
lovelyrwwr
- 48
- 0
I'm studying for the MCAT and this problem came up. The correct answer is D. However the explanation was very confusing.
The explanation is verbatim:
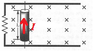
" Let's start by considering A. Using the right-hand rule on a current running through the wire in figure 2 shows you that the rod is pushed either left or right (depending on the direction of the current). This invalidates choice A. Magnetic flux does not tend to change. That is why as stated int he passage the current generated in a wire loop will orient itself so that its magnetic field opposes the induced change in flux--a condition described by Lenz's law. This invalidates choices B, C, and favors D. The best answer is choice D."
I cannot for the life of me understand how the right hand rule on the current through the wire in figure 2 shows you that the rod is either pushed left or right :(
View attachment delete.bmp
[/ATTACH]
The explanation is verbatim:
" Let's start by considering A. Using the right-hand rule on a current running through the wire in figure 2 shows you that the rod is pushed either left or right (depending on the direction of the current). This invalidates choice A. Magnetic flux does not tend to change. That is why as stated int he passage the current generated in a wire loop will orient itself so that its magnetic field opposes the induced change in flux--a condition described by Lenz's law. This invalidates choices B, C, and favors D. The best answer is choice D."
I cannot for the life of me understand how the right hand rule on the current through the wire in figure 2 shows you that the rod is either pushed left or right :(
View attachment delete.bmp
[/ATTACH]
Attachments
Last edited:
 )))))))))))))))))))))))))
)))))))))))))))))))))))))