Conservation of angular momentum

[WonderKitten]

Hi, I have the following problem:
A homogeneous disc with M = 1.78 kg and R = 0.547 m is lying down at rest on a perfectly polished surface. The disc is kept in place by an axis O although it can turn freely around it.
A particle with m = 0.311 kg and v = 103 m/s, normal to the disc's surface at the point of contact.
After the collision, the particle stays stuck to the impact point O'.
What's the angular velocity of the system after the collision?

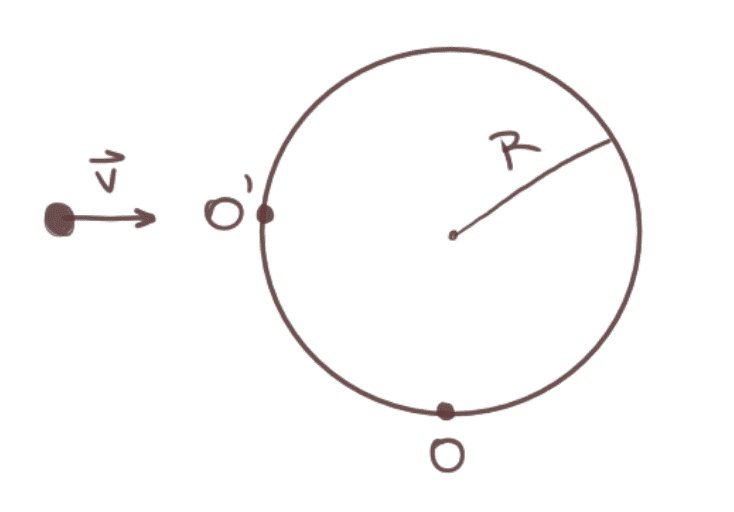
It might be a bit confusing as I had to translate the problem, sorry about that. I'm not entirely sure if the disc is rotating on it's x-axis or z-axis (y-axis?), and by the particle being 'normal to the disc's surface' I think it means it's perpendicular to the disc? Not sure what I should do with this information.

So, since the axis of rotation isn't on the center of mass:
I (disc) = MR²/2 + MR² = 3MR²/2
The distance from O' to O: (using pythagoras)
r = 0.774
I (particle) = mr²

Ip * vR = - (Id + Ip) * wf
solving for wf and substituting the values I get wf = -10.6.

This is wrong, apparently. Not sure why, I'm out of ideas. Could someone help me out? Thanks!

[Moderator's note: Moved from a technical forum and thus no template.]

 

[kuruman]

Your method is correct, recheck your calculations. I got a different answer. Also, why the negative sign? If your repeated calculation returns the same answer, please post it in more detail.

The disk is rotating about point O in the plane of the screen. The particle collides with the disk in a direction perpendicular to the rim, i.e. the velocity is directed towards the center of the disk. This allows you to write the angular momentum of the particle relative to point O as $L=mvR$ which I think is what you have done, but I am not sure.

 

[WonderKitten]

When the particle hits the disc it will begin rotating in the clockwise direction, that's why it's negative.
As for the calculations:
Ip = mr² = 0.186
Id = 3MR²/2 = 0.799
Ip + Id = 0.985
Ip * vR / Ip + Id = 10.6

If I use mVR = (Ip+Id)wf (as suggested by someone)
I get 17.8... but shouldn't I use 'mr²' instead of 'm'?
Thanks

Just saw your edit and I think that's it then? Thanks for the explanation on why it's mvR, got it.

 

[kuruman]

get 17.8... but shouldn't I use 'mr²' instead of 'm'?

That's the number I got. Use mr² instead of m in what expression? Angular momentum conservation says $$L_{\mathrm{before}}=L_{\mathrm{after}}$$ where$$L_{\mathrm{before}}=mvR; ~~L_{\mathrm{after}}=(I_d+I_p)\omega~~ \text{with} ~~I_d=\frac{3}{2}MR^2~~\text{and } I_p=m(2R^2).$$Perhaps you missed the point that the angular momentum of a particle is, by definition, the cross product $\vec L =\vec r \times \vec p$, See here for example. In the present case, $r ~\sin\theta =\text{constant}=R.$

 

[WonderKitten]

Perhaps you missed the point that the angular momentum of a particle is, by definition, the cross product $\vec L =\vec r \times \vec p$, See here for example. In the present case, $r ~\sin\theta =\text{constant}=R.$

Yep, that was it. Thank you!