- #1
knowNothing23
- 35
- 0
A pendulum consists of a 2.0-kg bob attached to a light 3.0-m-long
string. While hanging at rest with the string vertical, the bob is struck a sharp
horizontal blow, giving it a horizontal velocity of 4.5 m/s. At the instant the string
makes an angle of 30° with the vertical, what is (a) the speed, (b) the gravitational
potential energy (relative to its value is at the lowest point), and (c) the tension in
the string? (d) What is the angle of the string with the vertical when the bob
reaches its greatest height?
My problem is with the answer of c.)
The book shows a different answer.
Thank you.
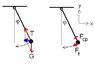
I have taken the free body diagram of the pendulum and the string, when the string forms 30 degrees with the vertical.
The net force sum of the "y" component:
[itex]\sumF[/itex]=Tcos(30)-mg=m(v^(2) )/ L , where "L" is the length of the string.
Solving for T:
T=(m/cos(30) )( v^(2)/L +g)
My answer is 32N.
string. While hanging at rest with the string vertical, the bob is struck a sharp
horizontal blow, giving it a horizontal velocity of 4.5 m/s. At the instant the string
makes an angle of 30° with the vertical, what is (a) the speed, (b) the gravitational
potential energy (relative to its value is at the lowest point), and (c) the tension in
the string? (d) What is the angle of the string with the vertical when the bob
reaches its greatest height?
My problem is with the answer of c.)
The book shows a different answer.
Thank you.
The Attempt at a Solution
I have taken the free body diagram of the pendulum and the string, when the string forms 30 degrees with the vertical.
The net force sum of the "y" component:
[itex]\sumF[/itex]=Tcos(30)-mg=m(v^(2) )/ L , where "L" is the length of the string.
Solving for T:
T=(m/cos(30) )( v^(2)/L +g)
My answer is 32N.