Conservation of Energy, Simple Harmonic Motion

[jacksonpeeble]

Homework Statement

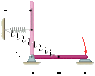
A 0.200-m uniform bar has a mass of 0.790 kg and is released from rest in the vertical position, as the drawing indicates. The spring is initially unstrained and has a spring constant of k = 20.0 N/m. Find the tangential speed with which end A strikes the horizontal surface.

Homework Equations

E_up=mgh=E_down=.5Iw²+.5ky²

\sqrt{3(mgL-ky^{2}}

The Attempt at a Solution

\sqrt{.1^{2}+.2^{2}}-.1=.124

\sqrt{\frac{3(.79 kg)(9.8 m/s/s)(.2 m)-(20 N/m)(.124 m)^{2}}{.790}}=2.343 m/s

I think that I went about this the right way and simply made an arithmetic error or plugged in something incorrect. Any help will be greatly appreciated, as I must have this assignment completed by midnight.

 

[jacksonpeeble]

Any suggestions?

 

[Redbelly98]

Just saw this, looks like it's too late.

In the energy equation, you omitted the kinetic energy of the bar's center-of-mass, (1/2)mv². (v is the velocity of the center of the bar.)

 

[jacksonpeeble]

Just saw this, looks like it's too late.

In the energy equation, you omitted the kinetic energy of the bar's center-of-mass, (1/2)mv². (v is the velocity of the center of the bar.)

Thank you, I appreciate the help anyway so that I can do the problems in the future. I was able to turn in that problem later for partial credit - a friend helped me.

:]