Conservative force pairs

[Hajarmq]

Let F_ki be the force applied by a point mass i on a point mass k. This force depends on the variables x_k and x_i which are the position vectors of respectively k and i (to simplify let´'s consider this in 1 dimension). Suppose this force is conservative. Then, according to my course and wikipedia, it can be written as:

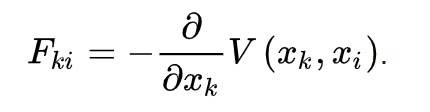My question is: why is the partial derivative with respect to x_k, the coordinate of the point mass the force is applied on? Why not x_i, or both x_i and x_k, since the potential depends on both of them?

 

[vanhees71]

By definition the force on a particle is, for a conservative force, given as the gradient of a potential wrt. the position of that particle.

If you have a socalled two-body force, the potential for a system of $N$ point particles is given by
$$V(\vec{x}_1,\ldots,\vec{x}_2)=\sum_{j<k} V_{jk}(\vec{x}_j,\vec{x}_k).$$
The force on the $i$-th particle then is
$$\vec{F}_i=-\vec{\nabla} V(\vec{x}_1,\ldots,\vec{x}_N)=-\sum_{k \neq i} \vec{\nabla}_i V_{ik}(\vec{x}_i,\vec{x}_k).$$

 

[kuruman]

By definition the force on a particle is, for a conservative force, given as the gradient of a potential wrt. the position of that particle.

If you have a socalled two-body force, the potential for a system of $N$ point particles is given by
$$V(\vec{x}_1,\ldots,\vec{x}_2)=\sum_{j<k} V_{jk}(\vec{x}_j,\vec{x}_k).$$
The force on the $i$-th particle then is
$$\vec{F}_i=-\vec{\nabla} V(\vec{x}_1,\ldots,\vec{x}_N)=-\sum_{k \neq i} \vec{\nabla}_i V_{ik}(\vec{x}_i,\vec{x}_k).$$

I think the answer is a bit more subtle. In two-body forces one body is at the "source" (primed) coordinates and the other is at the "field" (unprimed) coordinates. Then one writes,$$V[(\vec{x}_1-\vec{x}'_1),\ldots,(\vec{x}_N-\vec{x}'_N)]=\sum_{j<k} V_{jk}[(\vec{x}_j-\vec x'_j),(\vec{x}_k-\vec x'_k)].$$In order to find the force on the $i$th particle, derivatives need to be taken with respect to the unprimed field coordinates where the particle is.

In OP's equation $x_k$ is the field coordinate and $x_i$ the source coordinate. If this equation is in OP's course notes and Wikipedia (reference?), the meaning of the coordinates must have been given.

 

[Dale]

why is the partial derivative with respect to x_k, the coordinate of the point mass the force is applied on? Why not x_i, or both x_i and x_k, since the potential depends on both of them?

As mentioned above this is basically how $V$ is defined. To motivate that definition, let’s think about what we want $V$ to do.

We want the potential to tell us the work done on a particle. The work done on a given particle is given by $\vec F \cdot \Delta\vec x$ where $\vec F$ is a force acting on the given particle and $\Delta\vec x$ is the displacement of that particle.

So the work done on a particle is given by the force on that particle and the displacement of that particle. Therefore, the partial derivative in the definition of $V$ should be with respect to the position of the particle that the force is acting on, which is $x_k$

 

[vanhees71]

I think the answer is a bit more subtle. In two-body forces one body is at the "source" (primed) coordinates and the other is at the "field" (unprimed) coordinates. Then one writes,$$V[(\vec{x}_1-\vec{x}'_1),\ldots,(\vec{x}_N-\vec{x}'_N)]=\sum_{j<k} V_{jk}[(\vec{x}_j-\vec x'_j),(\vec{x}_k-\vec x'_k)].$$In order to find the force on the $i$th particle, derivatives need to be taken with respect to the unprimed field coordinates where the particle is.

In OP's equation $x_k$ is the field coordinate and $x_i$ the source coordinate. If this equation is in OP's course notes and Wikipedia (reference?), the meaning of the coordinates must have been given.

There are $N$ point particles, and the forces in Newtonian mechanics only depend on the positions of these $N$ point particles. What should thus the primed position vectors mean?

Of course you are right. Taking Galilei invariance of Newtonian spacetime into account the two-body forces must be central forces, i.e.,
$$V_{jk}(\vec{x}_j,\vec{x}_k)=V_{jk}(|\vec{x}_j-\vec{x}_k|)$$
due to homogeneity and isotropu of space. That the $V_{jk}$ also don't depend on $t$ is due to time-translation invariance.