Constrained Plane of Motion Problem

[RoyalFlush100]

Homework Statement

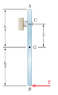
A uniform slender rod of length L = 1180 mm and mass m = 5.4 kg is suspended from a hinge at C. A horizontal force P of magnitude 75 N is applied at end B.

Determine the distance

for which the horizontal component of the reaction at C is zero.

I have attached the image below.

Homework Equations

M = Iα

The Attempt at a Solution

FBD:
W = mg = (5.4)(9.81) = 52.974 downwards, at G
Cy at C
75 N left, at B (already on the diagram)
Angular Acceleration at B?
Angular Velocity at B?

I'm kind of stuck at the setup and don't really know how to proceed beyond this.

 

[haruspex]

Angular Velocity at B?

The question is only concerned with the instantaneous circumstance, so there is as yet no velocity at B.
The will be accelerations. If the angular acceleration is α, what will be the linear acceleration of the mass centre?
What equations can you write relating forces to accelerations and torques to angular accelerations?

 

[zwierz]

https://en.wikipedia.org/wiki/Center_of_percussion

 

[RoyalFlush100]

The question is only concerned with the instantaneous circumstance, so there is as yet no velocity at B.
The will be accelerations. If the angular acceleration is α, what will be the linear acceleration of the mass centre?
What equations can you write relating forces to accelerations and torques to angular accelerations?

-Since there is no angular velocity the normal acceleration will be equal to 0.
-Likewise, the tangential acceleration will be equal to the product of r and α. However, I am unsure of the direction it will move in.
-Also since that is the total net force, ma = mrα = summation of all forces.
-Also, the torque will equal Iα + mad (the perpendicular d).

So I'm assuming I solve for I, which I think would be equal to (1/12)mL^2 = (1/12)(5.4 kg)(1.180 m)^2 = 0.531 kg*m^2. And that would act at the bar's center.
For the net force, I'm assuming I use this to solve for alpha (in terms of r). Also, I assume the tangental acceleration will be completely to the left, in which case:
mrα = P --> α = P/m/r = (75)/(5.4)/r = 13.889/r.

However, I'm not sure what else I can do from here. Was my assumption about the direction of the acceleration wrong? Was my inertia calculation wrong?

 

[haruspex]

the normal acceleration will be equal to 0.

I guess you mean the radial acceleration.

the tangential acceleration will be equal to the product of r and α.

That will be the linear acceleration of the rod's mass centre, yes.

mrα = P

Correct.

Not sure what you meant by your discussion of torque. For angular accelerations and torques you need to pick a reference axis. It can be any stationary point or the mass centre. If we take the pivot as reference, what is the torque from P about that? What is the moment of inertia of the rod about that? What equation does that give you?

 

[RoyalFlush100]

For angular accelerations and torques you need to pick a reference axis. It can be any stationary point or the mass centre. If we take the pivot as reference, what is the torque from P about that? What is the moment of inertia of the rod about that? What equation does that give you?

Okay so if I understand correctly, we need to sum the torques at C, to solve for r. So now two formulas:
mrα = P --> α = P/(mr)
τ = Iα + mar = (IP)/(mr) + P = (r+L/2)P
Is this setup correctly? Also, I'm unsure about how to calculate the moment of inertia. Is it simply (1/12)mr^2?

 

[haruspex]

Iα + mar = (IP)/(mr) + P

P=mrα, not mra.

moment of inertia. Is it simply (1/12)mr^2?

Yes.

 

[RoyalFlush100]

P=mrα, not mra.

Okay so in that case:
Iα + mar = (r+L/2)P
(1/12)(mr^2)α + mar = rP + PL/2
a = rα
(1/12)(mr^2)α + mαr^2 = rP + PL/2
α = P/(mr)
(1/12)(mr^2)P/(mr) + mPr^2/(mr) = rP + PL/2
(1/12)rP + rP = rP + PL/2
(1/12)r = L/2
r = 6L

Obviously that's not possible, so what did I mess up?

 

[haruspex]

Is it simply (1/12)mr^2?

Sorry, I did not check that properly. You do not mean r there. What should it be?

 

[RoyalFlush100]

Sorry, I did not check that properly. You do not mean r there. What should it be?

Got it, thanks!