- #1
Nexus99
- 103
- 9
- Homework Statement
- posted in solution
- Relevant Equations
- Conservation of angular momentum, kinetic energy etc.
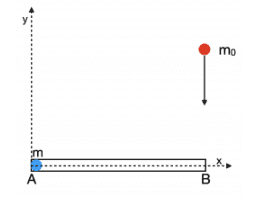
A hollow rod closed at the ends A and B, has mass M and length R. The rod is free
to rotate on a horizontal frictionless plane around the z axis passing through A
and coming out of the sheet. A body can slide without friction inside the cavity
point mass m.
Initially the rod is stationary and the mass m is placed, also stationary, at a distance
negligible but finished by A. A ball of mass m0, with velocity ##\vec{v_0}## = (0,-v0, 0), elastically hits it in B. Calculate:
1. the speed of the ball ##\vec{v_1}## and the angular speed ##\vec{\omega_i}## I of the rod immediately after the impact;
2. the impulse of the constraint reaction ##\vec{J}##
After the impact, the mass m starts up and reaches the end B. Calculate:
3. the angular speed of the rod ##\vec{\omega_{f}}## and the module of the speed ##v_f## of the mass m
with respect to the rod when m reaches B;
4. assuming that the mass m bounces elastically in B, calculate the speed
angle ##\vec{\omega_{A}}## of the rod when m returns to A;
In the event that the rod is not constrained to A and the impact is completely inelastic determine:
5. the equation of motion of the overall center of mass of the ##\vec{r_{CM}}## system;
6. the angular velocity ##\vec{\omega_{CM}}## with respect to an axis passing through the center of mass.
1) angular momentum and kinetic energy is conserved:
## -m_0 v_0 R = m_0 v_1 R + I \omega_1 ##
## \frac{1}{2} m_0 v_0^2 = \frac{1}{2} I \omega_{i}^2 + \frac{1}{2} m_0 v_1^2 ##
Solving the system i got:
## v_1 = \frac{(I-R^2 m_0) v_0}{I + R^2 m_0}##
## \omega_i = -\frac{2 R m_0 v_0}{I + R^2 m_0}##
where ## I = \frac{M R^2}{3} ##
## \vec{v_1} = (0,v_1,0)## and ##\vec{\omega_i} = (0,0,\omega_{i}) ##
2) Impulse of the costraint reaction = - Impulse generated by the ball
## J = -(m_0 v_1 - m_0 v_0) = \frac{2R^2 m_0^2 v_0}{I + R^2 m_0} ##
##\vec{J} = (0,J,0) ##
3) Angular momentum and kinetic energy is conserved
## I \omega_{i} = I \omega_{f} + m v_{f} R##
## \frac{1}{2} I \omega_i^2 = \frac{1}{2} I \omega_f^2 + \frac{1}{2} m v_f^2 ##
and i got
##v_f = \frac{2 I R \omega_i}{I + R^2m_0} ##
##\omega_f = \frac{\omega_{i}(I - R^2 m_0 }{I + R^2m_0} ##
##\vec{\omega_{f}} = (0,0, \omega_{f}) ##
4) momentum and kinetic energy is conserved
## - m v_f = m v_A ##
## \frac{1}{2} I \omega_f^2 + \frac{1}{2} m v_f^2 = \frac{1}{2} m v_A^2 + \frac{1}{2} I \omega_A^2##
and i got
##\omega_f = \omega_A##
##\vec{\omega_A} = (0,0, - \omega_f )##
5) i don't know, i think that ##x_{CM}## is constant since total ##p_{x}## is constant and equal to 0
So i would say ##x_{CM} = \frac{R(2m_0 + M)}{2(m + M + m_0)}##
Neither the momentum along the y-axis nor the kinetic energy is conserved, so i think that the CM along y-axis is moving uniform linear motion but i don't know how to find ##v_{y_{CM}}##
Can you help me?
to rotate on a horizontal frictionless plane around the z axis passing through A
and coming out of the sheet. A body can slide without friction inside the cavity
point mass m.
Initially the rod is stationary and the mass m is placed, also stationary, at a distance
negligible but finished by A. A ball of mass m0, with velocity ##\vec{v_0}## = (0,-v0, 0), elastically hits it in B. Calculate:
1. the speed of the ball ##\vec{v_1}## and the angular speed ##\vec{\omega_i}## I of the rod immediately after the impact;
2. the impulse of the constraint reaction ##\vec{J}##
After the impact, the mass m starts up and reaches the end B. Calculate:
3. the angular speed of the rod ##\vec{\omega_{f}}## and the module of the speed ##v_f## of the mass m
with respect to the rod when m reaches B;
4. assuming that the mass m bounces elastically in B, calculate the speed
angle ##\vec{\omega_{A}}## of the rod when m returns to A;
In the event that the rod is not constrained to A and the impact is completely inelastic determine:
5. the equation of motion of the overall center of mass of the ##\vec{r_{CM}}## system;
6. the angular velocity ##\vec{\omega_{CM}}## with respect to an axis passing through the center of mass.
1) angular momentum and kinetic energy is conserved:
## -m_0 v_0 R = m_0 v_1 R + I \omega_1 ##
## \frac{1}{2} m_0 v_0^2 = \frac{1}{2} I \omega_{i}^2 + \frac{1}{2} m_0 v_1^2 ##
Solving the system i got:
## v_1 = \frac{(I-R^2 m_0) v_0}{I + R^2 m_0}##
## \omega_i = -\frac{2 R m_0 v_0}{I + R^2 m_0}##
where ## I = \frac{M R^2}{3} ##
## \vec{v_1} = (0,v_1,0)## and ##\vec{\omega_i} = (0,0,\omega_{i}) ##
2) Impulse of the costraint reaction = - Impulse generated by the ball
## J = -(m_0 v_1 - m_0 v_0) = \frac{2R^2 m_0^2 v_0}{I + R^2 m_0} ##
##\vec{J} = (0,J,0) ##
3) Angular momentum and kinetic energy is conserved
## I \omega_{i} = I \omega_{f} + m v_{f} R##
## \frac{1}{2} I \omega_i^2 = \frac{1}{2} I \omega_f^2 + \frac{1}{2} m v_f^2 ##
and i got
##v_f = \frac{2 I R \omega_i}{I + R^2m_0} ##
##\omega_f = \frac{\omega_{i}(I - R^2 m_0 }{I + R^2m_0} ##
##\vec{\omega_{f}} = (0,0, \omega_{f}) ##
4) momentum and kinetic energy is conserved
## - m v_f = m v_A ##
## \frac{1}{2} I \omega_f^2 + \frac{1}{2} m v_f^2 = \frac{1}{2} m v_A^2 + \frac{1}{2} I \omega_A^2##
and i got
##\omega_f = \omega_A##
##\vec{\omega_A} = (0,0, - \omega_f )##
5) i don't know, i think that ##x_{CM}## is constant since total ##p_{x}## is constant and equal to 0
So i would say ##x_{CM} = \frac{R(2m_0 + M)}{2(m + M + m_0)}##
Neither the momentum along the y-axis nor the kinetic energy is conserved, so i think that the CM along y-axis is moving uniform linear motion but i don't know how to find ##v_{y_{CM}}##
Can you help me?
Last edited by a moderator: