- #1
Davidllerenav
- 424
- 14
Homework Statement
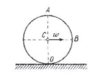
A cylinder rolls without slippage on a horizontal plane. The radius of the cylinder is equal to r. Find the radious of curvature of the trajectory of points A and B.
Homework Equations
- Ciruclar motion equations.
- ##R=\frac{1}{C}##
The Attempt at a Solution
First I drew the velocity of A and B, as well as the angular acceleration of both like this:
After that I used the formula for the radious of cuvature ##R=\frac{1}{C}=\frac{ds}{d\varphi}\Rightarrow ds=Rd\varphi \Rightarrow d\varphi=\frac{ds}{R}=\frac{vdt}{R}\Rightarrow \frac{d\varphi}{dt}=\frac{v}{R}=\omega##. Then, I used the angular acceleration formula ##a_{n}=\frac{v^2}{R}=\omega^2 R##.
After that I attempted to find the radious of A:
##v_A=\omega R_A##
##a_{nA}=\frac{v_A^2}{R_A}\Rightarrow R_A=\frac{v_A^2}{a_{nA}}=\frac{\omega^2R_A^2}{a_{nA}}##
After that I don't know whta to do, is that it? Or do I have to do something else?