B Constrains in E8xE8 heterotic superstring theory

[bluecap]

Can someone at least gives a summary of the constrains in the E8xE8 heterotic superstring theory? Many sources are mostly outdated that was written decades ago when not much research were done yet in superstring theory. So is E8xE8 already refuted? Or to what degrees and what constrains? I need updates about this because do you know E8xE8 is a favorite among many because they could create complex numerology out of it (why are there so much interesting patterns in E8xE8). For example:

 

[VIctor Medvil]

No, Heterotic string theory is one of the many version of String Theory that construct M-Theory and is the completely Invariant form being a E8 x E8 = SO(32) Killing Vector system with extremely complex math involved in its calculations, which none of the different String Versions of M-Theory are more or less valid just different mathematical constructs of the same-thing. Here is links you may find interesting.

Introduction
https://math.berkeley.edu/~kwray/papers/string_theory.pdf

More Detailed
http://stringworld.ru/files/Becker_K.__Becker_M.__Schwarz_J.H.__String_theory_and_M-theory.pdf

Detailed Constraints of Heterotic String on Tension of Strings.
https://link.springer.com/article/10.1007/JHEP08(2016)133Those Interesting patterns you see are the "Lie Groups" a type of spinor group which is actually a type of solution to the "probability space" or Quantum states of QM in picture form in String Theory.

Look at this... Similar to your Lie group, the Polytope in the first picture you linked? This S orbital?

 

[bluecap]

No, Heterotic string theory is one of the many version of String Theory that construct M-Theory and is the completely Invariant form being a E8 x E8 = SO(32) Killing Vector system with extremely complex math involved in its calculations, which none of the different String Versions of M-Theory are more or less valid just different mathematical constructs of the same-thing. Here is links you may find interesting.

Introduction
https://math.berkeley.edu/~kwray/papers/string_theory.pdf

More Detailed
http://stringworld.ru/files/Becker_K.__Becker_M.__Schwarz_J.H.__String_theory_and_M-theory.pdf

Detailed Constraints of Heterotic String on Tension of Strings.
https://link.springer.com/article/10.1007/JHEP08(2016)133Those Interesting patterns you see are the "Lie Groups" a type of spinor group which is actually a type of solution to the "probability space" or Quantum states of QM in picture form in String Theory.

Look at this... Similar to your Lie group, the Polytope in the first picture you linked? This S orbital?

View attachment 220226

What are the constraints of supersymmetry between the e8 normal baryonic particles and the e8' shadow matter baryonic particles? Remember they are just duplicates.. one is left handed.. one is right handed (shadow matter)... and even though they are not connected by the electroweak and strong force.. couldn't the supersymmetry be coupled by some kind of 5th force between existing low energy normal and shadow matter? Would there be rules that can forbid this union?

 

[VIctor Medvil]

What are the constraints of supersymmetry between the e8 normal baryonic particles and the e8' shadow matter baryonic particles? Remember they are just duplicates.. one is left handed.. one is right handed (shadow matter)... and even though they are not connected by the electroweak and strong force.. couldn't the supersymmetry be coupled by some kind of 5th force between existing low energy normal and shadow matter? Would there be rules that can forbid this union?

Well, Symmetry or Super-symmetry must be across a property or set of properties of nature that has a Standard/Normal and Opposite/inverse form of itself whether that is a force or whatever property has a Anti-particle across it, It is possible to have more forces than the 4 standard forces of nature being Electromagnetism,SNF,WNF, and Gravitational, but it is not generally accepted that there are more, personally, I think all things in this Universe can be explained as functions of the current 4 forces and their properties which is shared by mainstream science 99% of the time. You could speculate about it forever, but without evidence it is baseless hypothesizing. For instance, I could construct a model with a billion forces and a trillion Ultra-Symmetric particle types across everything but without evidence that there are a billion forces and a trillion states of those forces in the universe, it is baseless.

When I model Dark matter versus normal matter in "Toy Models and Theoretical models" that I construct, I do it as super-symmetry across flavour a property of the Higgs Mechanism on the Weak Nuclear Force denoted by the variable "Y", but you could do it many different ways for example which explains the same thing this does in a different model's math, This is just one of those things they did because it seemed to make sense in the context of Heterotic String's Math to explain the observed states of matter, in my opinion.

So, the actual constraints are what types of matter and particles do we actually observe in the universe and what causes them. The easiest way to explain it in the context of "B".

Think of Matter and Antimatter with the opposite Electric charge and opposite "Color Charge" it is the same idea applied in a different area upon a different property these "Shadow Matter Particles" being across Spin Number.

 

[bluecap]

Well, Symmetry or Super-symmetry must be across a property or set of properties of nature that has a Standard/Normal and Opposite/inverse form of itself whether that is a force or whatever property has a Anti-particle across it,

So why can't left handed normal baryonic matter be super partnered with right handed shadow baryonic matter?

It is possible to have more forces than the 4 standard forces of nature being Electromagnetism,SNF,WNF, and Gravitational, but it is not generally accepted that there are more, personally, I think all things in this Universe can be explained as functions of the current 4 forces and their properties which is shared by mainstream science 99% of the time. You could speculate about it forever, but without evidence it is baseless hypothesizing. For instance, I could construct a model with a billion forces and a trillion Ultra-Symmetric particle types across everything but without evidence that there are a billion forces and a trillion states of those forces in the universe, it is baseless.

When I model Dark matter versus normal matter in "Toy Models and Theoretical models" that I construct, I do it as super-symmetry across flavour a property of the Higgs Mechanism on the Weak Nuclear Force denoted by the variable Y, but you could do it many different ways for example which explains the same thing this does in a different model's math, This is just one of those things they did because it seemed to make sense in the context of Heterotic String's Math to explain the observed states of matter, in my opinion.

So, the actual constraints are what types of matter and particles do we actually observe in the universe?

Have you come across phase transitions (or symmetry breaking) that occurs not due to thermal effects.. to illustrate the point... in electroweak.. it splits into separate forces when the temperature lowers... but is there no mechanism where you can initiate phase transition that is not related to thermal in the low energy sector (or even high energy one). For example we can say that as the Big Bang occurs and before the temperature gets lowered.. there is another kind of phase transition invariant to temperature.. can you give any example that is used by physicists at arxiv?

Are you a physicist? Thanks a lot.

 

[VIctor Medvil]

So why can't left handed normal baryonic matter be super partnered with right handed shadow baryonic matter?
Have you come across phase transitions (or symmetry breaking) that occurs not due to thermal effects.. to illustrate the point... in electroweak.. it splits into separate forces when the temperature lowers... but is there no mechanism where you can initiate phase transition that is not related to thermal in the low energy sector (or even high energy one). For example we can say that as the Big Bang occurs and before the temperature gets lowered.. there is another kind of phase transition invariant to temperature.. can you give any example that is used by physicists at arxiv?

Are you a physicist? Thanks a lot.

They cannot be partner due to different interactions than standard matter.

Sure, Here is a paper about WIMPs, which is the form I was speaking about but on ARXIV. but there are many possible candidates for Dark Matter.

https://arxiv.org/abs/1707.06277

I do not exactly know whether or not there are ones not related to Thermal/Energy change myself other than neutralization to a property to 0, I have only ever seen symmetry breaks due to change in energy or neutralization of a property to 0 or a neutral state myself.

Biophysicist, I did many years as a Pure Physics major, but decided I liked Biophysics better, but still love to model Pure physics too.

 

[bluecap]

They cannot be partner due to different interactions than standard matter.

In shadow/mirror matter concept.. the masses were identical and even the forces were identical to normal baryonic universe except they are shadow forces (like dark photons) that only interact with the shadow matter. So it is not possible to have mediator particles or forces that can bind the two in some kind of portal scenario for example via the higgs portal? So no one really use the normal and shadow matter as supersymmetric partners?

Sure, Here is a paper about WIMPS, which is the form I was speaking about but on ARXIV. but there are many possible candidates for Dark Matter.

https://arxiv.org/abs/1707.06277

I do not exactly know whether or not there are ones not related to Thermal/Energy change myself other than neutralization to a property to 0, I have only ever seen symmetry breaks due to change in energy or neutralization of a property to 0 or a neutral state myself.

Biophysicist, I did many years as a Pure Physics major, but decided I liked Biophysics better, but still love to model Pure physics too.

Can you give example what you meant by neutralization to a property to 0? Let's wait for the experts (like Urs) to share if there are none thermal mode of phase transition.

 

[VIctor Medvil]

In shadow/mirror matter concept.. the masses were identical and even the forces were identical to normal baryonic universe except they are shadow forces (like dark photons) that only interact with the shadow matter. So it is not possible to have mediator particles or forces that can bind the two in some kind of portal scenario for example via the higgs portal? So no one really use the normal and shadow matter as supersymmetric partners?
Can you give example what you meant by neutralization to a property to 0? Let's wait for the experts (like Urs) to share if there are none thermal mode of phase transition.

Yes, when Electric Charge of matter and antimatter meet that are equal and opposite changing the form of the particles to photons or other particles causing a symmetry break upon Electric charge like in the scenario of Positrons and Electrons meeting making Electric Charge neutral photons of equal Energy-mass from the previously two (+1,-1) Electric charged particles's Energy-mass.

Photons being a neutral state of Energy-mass for Electric charge or in a 0 State of Electric Charge.

 

[bluecap]

Yes, when Electric charge of matter and antimatter meet that are equal and opposite changing the form of the particles to photons or other particles causing a symmetry break upon charge like in the scenario of Positrons and Electrons meeting making neutral photons from previously two (+1,-1) charged particles.

View attachment 220247

Photons being a neutral state or 0 State of Charge.

Example of non-thermal symmetry breaking are spinning tops where you make it fall to certain direction.. but in the case of particle physics SU(2), U(1).. I guess it's all related to temperature.. but you know the concept of catalysts in biochemistry.. I wonder if there are particles or mediator forces that can serve as catalysts able to change symmetric state.. maybe I need to ask this in separate thread at the high energy forum...

Back to the main topic of this thread. If supersymmetry won't be detected at all scale in LHC and 50 years onwards.. could e8xe8 heterotic superstring theory still be viable?

 

[VIctor Medvil]

Example of non-thermal symmetry breaking are spinning tops where you make it fall to certain direction.. but in the case of particle physics SU(2), U(1).. I guess it's all related to temperature.. but you know the concept of catalysts in biochemistry.. I wonder if there are particles or mediator forces that can serve as catalysts able to change symmetric state.. maybe I need to ask this in separate thread at the high energy forum...

Back to the main topic of this thread. If supersymmetry won't be detected at all scale in LHC and 50 years onwards.. could e8xe8 heterotic superstring theory still be viable?

There are particles that serve the purpose of mediators W+,W- and Z bosons upon the Weak Nuclear Force that mediate transitions between states of the other forces in the Standard model.

Yes, Heterotic string is still viable as M-Theory is still a candidate for the correct structural model of the universe being that Heterotic String is apart of M-theory until M-Theory is ruled out neither is Heterotic String.

 

[bluecap]

There are particles that serve the purpose of mediators W+,W- and Z bosons upon the Weak Nuclear Force that mediate transitions between states of the other forces in the Standard model.

Yes, Heterotic string is still viable as M-Theory is still a candidate for the correct structural model of the universe being that Heterotic String is apart of M-theory until M-Theory is ruled out neither is Heterotic String.

What's M-theory or Superstring Theory like without any supersymmetric particles. I read in wiki: https://en.wikipedia.org/wiki/Superstring_theory

"Superstring theory is an attempt to explain all of the particles and fundamental forces of nature in one theory by modeling them as vibrations of tiny supersymmetric strings.

'Superstring theory' is a shorthand for supersymmetric string theory because unlike bosonic string theory, it is the version of string theory that accounts for both fermions and bosons and incorporates supersymmetry to model gravity."

So if there is are supersymmetric particles.. then shouldn't it not be called superstrings.. then what name should be called for these strings? Non-superstrings Theory? What do you think?

 

[VIctor Medvil]

Whatever you would like glad to have answered your question deep enough that this is all you have to ask, I would just call them "Strings" and the Super-symmetric ones "Super-strings" but whatever you would like as long as you get your meaning across efficiently, which is the purpose of language structure and Standardized definitions of words.

 

[bluecap]

Whatever you would like glad to have answered your question deep enough that this is all you have to ask, I would just call them "Strings" and the Super-symmetric ones "Super-strings" but whatever you would like as long as you get your meaning across efficiently, which is the purpose of language structure and Standardized definitions of words.

Ok.. but unforunately even these strings may just be emergent.. As Smolin wrote "it seems that any acceptable quantum theory of gravity, whatever its ultimate formulation, is likely to reduce to a perturbative string theory in the appropriate limit.".

string theory still has background where the strings can move or vibrate.. nature must and better be fully background independent (no prior geometry) where spacetime and the strings are created at same time.. so by the nature of strings it automatically has spacetime... therefore superstrings are just emergent of something.. even non-perturbative AdS/CFT has limitation in that it is not our space.. maybe we still have a long way to go.. this is why we must really based our search on more experimental signature or data whatever form it may take... not guesswork. I'll watch more video at youtubes to gain more understanding. Thanks for sharing.

 

[VIctor Medvil]

Ok.. but unforunately even these strings may just be emergent.. As Smolin wrote "it seems that any acceptable quantum theory of gravity, whatever its ultimate formulation, is likely to reduce to a perturbative string theory in the appropriate limit.".

string theory still has background where the strings can move or vibrate.. nature must and better be fully background independent (no prior geometry) where spacetime and the strings are created at same time.. so by the nature of strings it automatically has spacetime... therefore superstrings are just emergent of something.. even non-perturbative AdS/CFT has limitation in that it is not our space.. maybe we still have a long way to go.. this is why we must really based our search on more experimental signature or data whatever form it may take... not guesswork. I'll watch more video at youtubes to gain more understanding. Thanks for sharing.

I cannot go any deeper on these forums without risking a ban as I know I would a go away from "Mainstream Physics" as I did, Look me Up Vmedvil on google.com which was banned here for creative math in SR/GR before something to do with using QM in GR and SR equations to solve a few questions. I have many possible models of this subject in the context of String Theory and Quantum Gravity, I have gone into great deal the limits of it and details of String Theory in many posts and their possible meanings for physics, otherwise, continue to watch youtube videos which are probably less accurate, but yes, it must all have strict evidence to support it for the continuity of physics, it must be accurate model of the universe meaning conforming to its rules that are in place.

But, I will leave you with this, What if the movements/vibrations of Strings are what generate what we call "Space-time" as the connectors of Space-time being a cause not a effect of it.

 

[bluecap]

Victor.. can you help me with something. First let's stick to our topics and not mention anything else lest we be banned.
There are thousands and thousands of superstring papers written with almost all variations and possibilities. There is one particular that I'm interested in because it explains reality better (has more degrees of freedom) but some concepts confused me. According to one Phillips, he said superstrings are themselves the product of compactification of 11-branes embedded in 26-dimensional space-time. And there are certain other fields existing in the 15 higher dimensions outside these branes that play no part in the interactions between superstrings, which are therefore supersymmetric strings confined to a 10-dimensional space-time as projections of a higher-dimensional object. Let's stop at this description as these are general descriptions and can be understood by experts.

I'm a bit confused with something. It's the most sophisticated version of e8xe8. He said superstrings are products of compactification of 11-branes embedded in 26-dimensional spacetime. Since you are very good in graphics. Can you illustrate this? However, later he described supersymmetric strings as confined to a 10-dimensional space-time as projections of a higher-dimensional object. Why did he mention 11-branes then 10-dimensional space-time? How can the 11-branes fit into the 10-dimensional spacetime? Based on your very familiary with the concepts. Does it mean the 26 dimensional spacetime enclose both the 11 branes superstrings floating in 10 dimensional spacetime? Or does the 26 dimension only correspond to the superstring branes ingredients and not being part of the higher-dimensional object where the 10-dimensional space-time is projected?

Many superstring experts are bored to respond to newbies because the questions are so basic. So hope you can elaborate more details about how superstrings can be made of branes and at the same time how they can be confined to certain D-dimensional spacetime as projections of a higher-dimensional object. Let's strictly focus on this without getting outside the topic so we won't be banned. Thanks.

 

[VIctor Medvil]

Well, in String Theory, the it is a smooth Reimann manifold type which means it is a differential manifold meaning it is a geometric differential equation basically, so how is it possible for 11-D strings to fit on 10-D space-time, well that is due to the fact that it can bend in 11 different ways or "Degrees of Freedom", being 11 properties effect its shape. If you have taken differential geometry or Multi-variable calculus you will fully understand what I am saying but for those that don'tLet's first start with the Idea of Gaussian curvature "K" of a Volume's Surface over (X,Y,Z)

Morphisms on a Smooth Riemann Manifold of p to q over M being a surface over multiple changing variables.

Morphism over L = Z with a change in several Variables in Smooth Riemann Manifold

Higher Dimensional Morphism over many variables 11, in this case, Calabi Yau Manifold for String Theory at every point of space like "SR Light cones" in GR.

That is how it is possible those "Degrees of freedom" are just variables that effects its shape like K in Gaussian Curvature.

 

[bluecap]

before symmetry breaking.. electroweak SU(2)xU(1):
SU(2) weak-isopin which has 3 generators and 3 massless force-field quanta: W+, W-, W0
U(1) weak hypercharge has 1 generator and B0

after symmetry breaking.. We have the W+, W-, Z and photon

For the strong force SU(3) which eight generators, this means that there are thus eight gauge fields or gluons
So far these are all real fields...

Now for E8xE8.. does anyone seriously think there are 248 gauge fields?! Where are they? do they actually exist?
Could these 248 E8xE8 gauge fields being unseen put constrains on the E8xE8.. or does it mean they couldn't be real but somehow cancel each other out? Is there a mathematical operation that can cancel majority of the 248 gauge fields out? This questions goes the same for the GUT SU(5).. does every Lie Group generators be in the form of real gauge field that needs to exist??

 

[lpetrich]

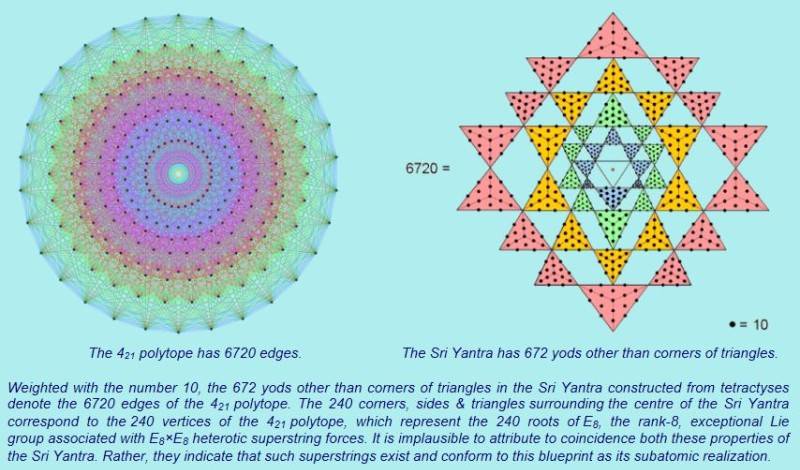
E8*E8 has 496 gauge modes, with each E8 having 248 of them. It is possible to get the Standard Model out of E8 and its fundamental multiplet, 248. It is also the E8 adjoint multiplet, the multiplet where each member corresponds to an algebra generator. Something only true of E8.

E8 -> E6*SU(3)
248 -> (78,1) + (1,8) + (27,3) + (27*,3*)

I've also seen
E8 -> SO(10)*SU(4)
248 -> (45,1) + (1,15) + (16,4) + (16*,4*) + (10,6)

The possible paths from E6 to the Standard Model have been abundantly explored by GUT model builders. Here are some:

E6 -> SO(10)*U(1)
27 -> (16,1/3) + (10-2/3,) + (1,4/3)
27* -> (16*,-1/3) + (10,2/3) + (1,-4/3)
78 -> (45,0) + (1,0) + (16,-1) + (16*,1)

SO(10) -> SU(5)*U(1)
16 -> (10,-1/4) + (5*,3/4) + (1,-5/4)
16* -> (10*,1/4) + (5,-3/4) + (1,5/4)
10 -> (5,1/2) + (5*,-1/2)
45 -> (24,0) + (1,0) + (10,1) + (10*,-1)

SU(5) -> SU(3)*SU(2)*U(1) (Standard Model)
5 -> (3,1,2/5) + (1,2,-3/5)
5* -> (3*,-1,2/5) + (1,2,3/5)
10 -> (3,2,-1/5) + (3*,1,4/5) + (1,1,-6/5)
10* -> (3*,2,1/5) + (3,1,-4/5) + (1,1,6/5)
24 -> (8,1,0) + (1,3,0) + (1,1,0) + (3,2,1) + (3*,2,-1)SO(10) -> SO(6)*SO(4) = SU(4)*SU(2)*SU(2)
16 -> (4,2,1) + (4*,1,2)
16* -> (4,1,2) + (4*,2,1)
10 -> (6,1,1) + (1,2,2)
45 -> (15,1,1) + (1,3,1) + (1,1,3) + (6,2,2)

SU(4) -> SU(3)*U(1)
4 -> (3,1/4) + (1,-3/4)
4* -> (3*,-1/4) + (1,3/4)
15 -> (8,0) + (1,0) + (3,1) + (3*,-1)

SU(2) -> U(1)
2 -> (1/2) + (-1/2)
3 -> (1) + (0) + (-1)E6 -> SU(3)^3
27 -> (3,3*,1) + (1,3,3*) + (3*,1,3)
27* -> (3*,3,1) + (1,3*,3) + (3,1,3*)
78 -> (8,1,1) + (1,8,1) + (1,1,8) + (3,3,3) + (3*,3*,3*)

SU(3) -> SU(2)*U(1)
3 -> (2,1/3) + (1,-2/3)
3* -> (2,-1/3) + (1,2/3)
8 -> (3,0) + (1,0) + (2,1) + (2,-1)So while one can get from E8 to the Standard Model, doing so requires some rather complicated symmetry breaking. In E8*E8 heterotic-string models, this is done by the compactification of six of the ten space-time dimensions. Their compactification's topology then induces symmetry breaking, and one can get some approximation of the Standard Model with suitable topology.

 

[arivero]

More Detailed
http://stringworld.ru/files/Becker_K.__Becker_M.__Schwarz_J.H.__String_theory_and_M-theory.pdf

Perhaps also Ibañez's https://www.amazon.com/dp/0521517524/?tag=pfamazon01-20 ? There is not a lot about E8xE8, but it is a pheno textbook.