Construct the Lagrangian for the system

[proton4ik]

Homework Statement

Hello!
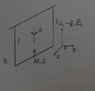
I have some problems with constructing Lagrangian for the given system:

(Attached files)

Homework Equations

The answer should be given in the following form: L=T-U=...

The Attempt at a Solution

I tried to construct the Lagrangian, but I'm not sure if I did it correctly:
$$\frac{M}{2} \left(\dot z^{2} + \dot x^{2} + \dot y^{2}\right) = T$$
$$ U=mgz $$
$$ x=L*{\cos{\varphi}},$$
$$y=L*{\sin{\varphi}},$$
$$z=l*(1-{\cos{\varphi}}) $$
$$- e l q \sin{\left (\varphi \right )} - g l M \left(- \cos{\left (\varphi \right )} + 1\right) + \frac{L^{2} M}{2} \left(\dot {\varphi}^{2} + \left(- \cos{\left (\varphi \right )} + 1\right)^{2}\right) = {\mathcal {L}}$$I'll appreciate any help.

 

[PeterDonis]

Google drive links are not acceptable. Please post text and equations directly. You can use the PF LaTeX feature to help with equations:

https://www.physicsforums.com/help/latexhelp/

 

[TSny]

Please state the problem word for word (which should include a verbal description of the system).

 

[proton4ik]

Construct Lagrangian and Lagrange's equations of the second kind for the given mechanical system. Are the equations integrable by quadratures? If yes, find the quadratures.

Unfortunately, there is no verbal description of the system.. (

 

[PeterDonis]

Unfortunately, there is no verbal description of the system..

Is there any description of the system? Equations? Something?

If not, I have no idea how anyone would answer the question.

 

[proton4ik]

Is there any description of the system? Equations? Something?

If not, I have no idea how anyone would answer the question.

No, there's no description at all except for what's on the picture.

I suppose that it's a rod (L, M) suspended from two wires (l). There's probably a particle with charge q on the rod. And the system is rotating so the axis of rotation stays parallel to the wires.

 

[PeterDonis]

there's no description at all except for what's on the picture

Where is this problem from? I have never seen a textbook or other source give a picture with no accompanying words at all.

 

[PeterDonis]

I suppose that it's a rod (L, M) suspended from two wires (l). There's probably a particle with charge q on the rod. And the system is rotating so the axis of rotation stays parallel to the wires.

I would add that there appears to be a gravitational field pointing in the minus $z$ direction, and an electric field pointing in the plus $z$ direction. But I think all of this is tentative unless we can get more information about where this problem comes from.

 

[proton4ik]

I would add that there appears to be a gravitational field pointing in the minus $z$ direction, and an electric field pointing in the plus $z$ direction. But I think all of this is tentative unless we can get more information about where this problem comes from.

It's just an example of the exercise from the final exam. There are hundreds of similar pictures with the the same task in the examples.

 

[TSny]

Since the problem is from an exam, it should not be too complicated. So, I tend to think that the system acts like a pendulum where rod $L$ always remains horizontal and parallel to the x axis. The two massless strings (or rods) $l$ remain parallel to each other and swing parallel to the y-z plane [EDIT: or maybe the system swings parallel to the x-z plane]. The angle $\phi$ is the angle that each string makes to the vertical.

I agree with Peter that there is a vertically upward uniform electric field and a massless point charge at the center of rod $L$.

This is just my guess at the intended interpretation.

 

[PeterDonis]

Since the problem is from an exam, it should not be too complicated.

It's not a matter of complication; it's a matter of clarity. If that were all I saw on an exam, with no verbal description to tell me what the symbols mean, I would ask the examiner what they mean. (Unless the class in which this is an exam had provided a lot of context; perhaps the hundreds of similar pictures in the examples would help. But we can't see them here, so they're no help to us.)

 

[TSny]

It's not a matter of complication; it's a matter of clarity. If that were all I saw on an exam, with no verbal description to tell me what the symbols mean, I would ask the examiner what they mean.

Absolutely

(Unless the class in which this is an exam had provided a lot of context; perhaps the hundreds of similar pictures in the examples would help. But we can't see them here, so they're no help to us.)

Right

 

[TSny]

@proton4ik ,
You must have had your own interpretation of the problem in order to set up your equations in the first post. If you are interested in continuing with it, then let us know your interpretation and we might be able to help.

 

[proton4ik]

@proton4ik ,
You must have had your own interpretation of the problem in order to set up your equations in the first post. If you are interested in continuing with it, then let us know your interpretation and we might be able to help.

Yes, of course, I already stated my interpretation :)
Here it is:
I suppose that it's a rod (L, M) suspended from two wires (l). There's probably a particle with charge q on the rod. And the system is rotating so the axis of rotation stays parallel to the wires.

 

[TSny]

And the system is rotating so the axis of rotation stays parallel to the wires.

Bear with me, I can't visualize this. Would you mind describing the orientation and location of the axis of rotation a little more clearly? If the axis of rotation stays parallel to the wires, I take it that the wires stay parallel to one another. Does the axis of rotation itself change during the motion?

 

[proton4ik]

Bear with me, I can't visualize this. Would you mind describing the orientation and location of the axis of rotation a little more clearly? If the axis of rotation stays parallel to the wires, I take it that the wires stay parallel to one another. Does the axis of rotation itself change during the motion?

I think the axis of rotation is shown on the picture (in the centre of the system). It doesn't change itself. And the angular velocity is $$\dot {\varphi}$$.
Yes, of course, I think that wires should stay parallel to one another.

 

[TSny]

Does the entire system (including the upper supporting rod) rotate as a whole about the central vertical axis?

 

[proton4ik]

Does the entire system (including the upper supporting rod) rotate as a whole about the central vertical axis?

Yes, I think so. I also suppose that it's moving back and forth so the z-coordinate is changing.

 

[TSny]

Wouldn't any back and forth motion cause the wires to no longer be vertical (that is, the wires would not stay parallel to the axis of rotation)?

Also, is the angular velocity $\dot \varphi$ kept constant by an external agent, or is $\varphi$ a free variable (degree of freedom)?

 

[proton4ik]

Wouldn't any back and forth motion cause the wires to no longer be vertical (that is, the wires would not stay parallel to the axis of rotation)?

Also, is the angular velocity $\dot \varphi$ kept constant by an external agent, or is $\varphi$ a free variable (degree of freedom)?

You're right. In this case, I guess there's only rotational motion. But how to find the potential energy of the system then?
$\varphi$ is probably a free variable.

 

[TSny]

If the only freedom of motion is rotation of the whole system about the central vertical axis, then I can't see anything interesting happening.

My first interpretation was to assume the upper rod is fixed, but that the wires and lower rod can undergo "twisting" motion such that $\varphi$ is the angle of twist about a vertical axis through the center of the rod. The only motion of the center of the rod would be vertical motion where the height of the center of the rod would be a function of $\varphi$. It's not too hard to set up the Lagrangian for this case, but getting the equation of motion from the Lagrangian is a bit cumbersome (unless you assume small twisting oscillations so that you can use a small angle approximation). Likewise, the expression for the quadrature is messy. So, I didn't think that this interpretation would make a very good exam question. But, of course, who am I to make that decision?

 

[proton4ik]

If the only freedom of motion is rotation of the whole system about the central vertical axis, then I can't see anything interesting happening.

My first interpretation was to assume the upper rod is fixed, but that the wires and lower rod can undergo "twisting" motion such that $\varphi$ is the angle of twist about a vertical axis through the center of the rod. The only motion of the center of the rod would be vertical motion where the height of the center of the rod would be a function of $\varphi$. It's not too hard to set up the Lagrangian for this case, but getting the equation of motion from the Lagrangian is a bit cumbersome (unless you assume small twisting oscillations so that you can use a small angle approximation). Likewise, the expression for the quadrature is messy. So, I didn't think that this interpretation would make a very good exam question. But, of course, who am I to make that decision?

Your interpretation seems reasonable. Wouldn't Lagrangian look the same as I wrote in the question considering this interpretation?

 

[TSny]

Your interpretation seems reasonable. Wouldn't Lagrangian look the same as I wrote in the question considering this interpretation?

To what point do the coordinates $x$, $y$, and $z$ refer in your equations?

 

[proton4ik]

To what point do the coordinates $x$, $y$, and $z$ refer in your equations?

To the left end of the rod

 

[TSny]

To the left end of the rod

If the rod rotates about a vertical axis through its center, then the coordinates of the left end of the rod would not be given by your equations for $x$, $y$, and $z$. Also, the kinetic energy of the rod would not be given by 1/2 the mass times the square of the speed of the left end. There would be rotational kinetic energy plus translational kinetic energy due to vertical motion of the center of mass of the rod.