obad
- 12
- 0
Hi guys,
I need to determine the performance of a single expansion ramp nozzle (SERN) from CFD results with different nozzle pressure ratios (NPR). For some NPR the nozzle is overexpanded and for some underexpanded.
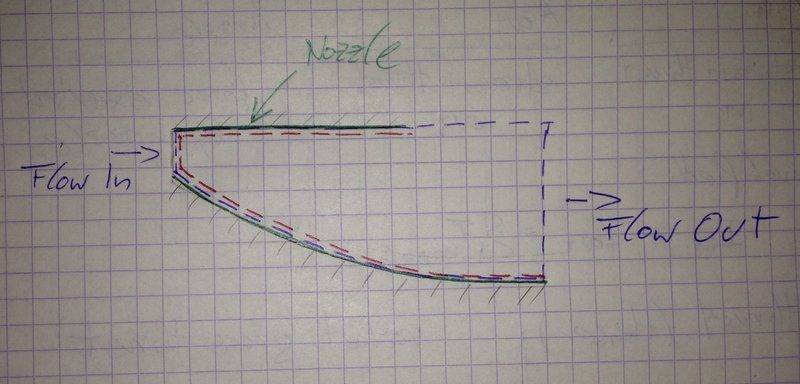
Now the impact of the control volume definition on especially the axial thrust is confusing me a lot. I attached a sketch of the nozzle with a control volume. The blue dashed line represents my control volume and the red dashed line just the inflow plane and the nozzle surface.
Now my understanding is, that the force acting on the nozzle surface is fixed by the pressure and shear acting on it. If there is an entrainment of external air into the nozzle (e.g. due to overexpanstion), then this entrainment would change the pressure and shear distribution over the surface. Subsequently the effect of an entrainment should already be included in the surface integrals of pressure and shear. And the difference in stream thrust of an arbitrarily chosen exit control volume and the inflow stream thrust should give exactly this surface force, right?
From my CFD simulations I can easily extract the pressure and shear force that are acting on the nozzle surface and I have the inflowing momentum (stream thrust). My first thought was, to simply add up the inflowing stream thrust to the force acting on the nozzle to get the outflowing streamthrust. Subsequently I would use this exit stream thrust for the performance analysis. That worked fine.
Then I thought that if I use the control volume given in the uploaded figure (blue dashed lines) and calculate the momentum flow over the exit portion of my control volume, the difference between this exit stream thrust and my inflow stream thrust should exactly yield the force that is acting on the body of the nozzle. But the problem is, that it doesn't match...
Cheers,
Obad
I need to determine the performance of a single expansion ramp nozzle (SERN) from CFD results with different nozzle pressure ratios (NPR). For some NPR the nozzle is overexpanded and for some underexpanded.
Now the impact of the control volume definition on especially the axial thrust is confusing me a lot. I attached a sketch of the nozzle with a control volume. The blue dashed line represents my control volume and the red dashed line just the inflow plane and the nozzle surface.
Now my understanding is, that the force acting on the nozzle surface is fixed by the pressure and shear acting on it. If there is an entrainment of external air into the nozzle (e.g. due to overexpanstion), then this entrainment would change the pressure and shear distribution over the surface. Subsequently the effect of an entrainment should already be included in the surface integrals of pressure and shear. And the difference in stream thrust of an arbitrarily chosen exit control volume and the inflow stream thrust should give exactly this surface force, right?
From my CFD simulations I can easily extract the pressure and shear force that are acting on the nozzle surface and I have the inflowing momentum (stream thrust). My first thought was, to simply add up the inflowing stream thrust to the force acting on the nozzle to get the outflowing streamthrust. Subsequently I would use this exit stream thrust for the performance analysis. That worked fine.
Then I thought that if I use the control volume given in the uploaded figure (blue dashed lines) and calculate the momentum flow over the exit portion of my control volume, the difference between this exit stream thrust and my inflow stream thrust should exactly yield the force that is acting on the body of the nozzle. But the problem is, that it doesn't match...
Cheers,
Obad