Alaskan Son
- 13
- 0
I'm looking for a little help here. I'm just a relatively regular Joe here though, so any complicated formulas are likely to go right over my head. What I'm trying to do is use the Ruby programming language to convert rise and run (slope) to degrees. See the attached screenshot...
View attachment 8617
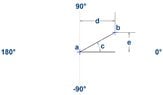
Assume x and y-axis are constant and that point a is always at 0,0. I want to use dimension d and e to obtain an angle in degrees. In this example:
d = 334.385384
e = 187.413131
I happen to know that angle c = approx. e° due to some tools I have available in my CAD program, but I really want to be able to plug d and e into a formula so I can get some automated feedback using some Ruby scripting. Ruby has an Arc Tangent function...
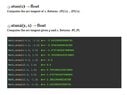
View attachment 8618
...but I'm really not sure how to use it. I tried using atan(e/d) but that results in 0.5108463979434283
I'd love if someone could help me understand what I'm doing wrong. Thanks.
View attachment 8617
Assume x and y-axis are constant and that point a is always at 0,0. I want to use dimension d and e to obtain an angle in degrees. In this example:
d = 334.385384
e = 187.413131
I happen to know that angle c = approx. e° due to some tools I have available in my CAD program, but I really want to be able to plug d and e into a formula so I can get some automated feedback using some Ruby scripting. Ruby has an Arc Tangent function...
View attachment 8618
...but I'm really not sure how to use it. I tried using atan(e/d) but that results in 0.5108463979434283
I'd love if someone could help me understand what I'm doing wrong. Thanks.