- #1
Qube
Gold Member
- 468
- 1
- Homework Statement
- Consider a headlamp that is measured to have an intensity of 35,000 candela at FMVSS 108 test point 1.5D, 2R. That is, 1.5 degrees below the horizontal axis and 2 degrees right of the vertical axis with respect to the lamp. On a completely unlit road, what is the maximum distance at which there is 5 lux illumination?
- Relevant Equations
- E = 10.76*(I/d^2)
We can solve for the maximum 5 lux illumination distance with the above equation.
E = 10.76*(35,000/d^2)
d = 275 feet (approximately).
However, the 5 lux illumination distance is not 275 feet. The 35,000 cd value is not an axial intensity value. It is at a point that is slightly down and to the right with regard to the intersection of the lamp's horizontal and vertical axes (H-V).
Therefore, we have to set up a right triangle as such:
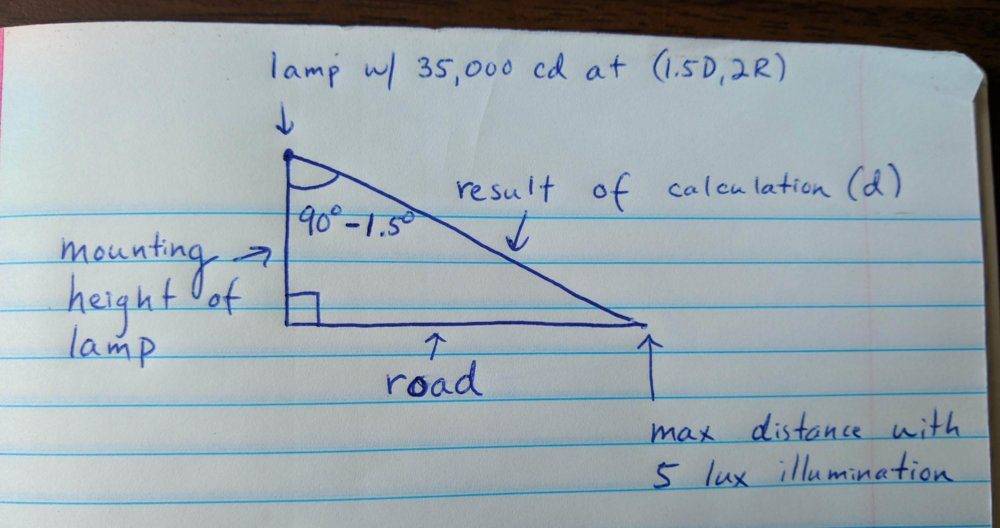
Is this the correct setup? Note that we cannot solve this problem as stated, since no mounting height of the lamp is given.
E = 10.76*(35,000/d^2)
d = 275 feet (approximately).
However, the 5 lux illumination distance is not 275 feet. The 35,000 cd value is not an axial intensity value. It is at a point that is slightly down and to the right with regard to the intersection of the lamp's horizontal and vertical axes (H-V).
Therefore, we have to set up a right triangle as such:
Is this the correct setup? Note that we cannot solve this problem as stated, since no mounting height of the lamp is given.