n3pix
- 15
- 1
I have a little question about converting Velocity formula that is derived as,
##\vec{V}=\frac{d\vec{r}}{dt}=\frac{dx}{dt}\hat{x}+\frac{dy}{dt}\hat{y}+\frac{dz}{dt}\hat{z}##
in Cartesian Coordinate Systems ##(x, y, z)##. I want to convert this into Polar Coordinate System ##(r, \theta)##.
##\vec{r}=r(t)\hat{r}(t)##
##\frac{\vec{r}}{dt}=\frac{d}{dt}[r(t)\hat{r}(t)]=\frac{dr}{dt}\hat{r}+r\frac{d\hat{r}}{dt}##
There are 2 methods to get velocity vector formula that is defined on Polar Coordinate Systems.
First method is like this,
##\hat{r}=\hat{x}\cos{\theta}+\hat{y}\sin{\theta}##
##\hat{\theta}=-\hat{x}\sin{\theta}+\hat{y}\cos{\theta}##
##\frac{d\hat{r}}{dt}=-\sin{\theta}\dot{\theta}\hat{x}+\cos{\theta}\dot{\theta}\hat{y}##
##\frac{d\hat{r}}{dt}=\dot{\theta}(-\sin{\theta}\hat{x}+\cos{\theta}\hat{y})##
##\frac{d\hat{r}}{dt}=\dot{\theta}(\hat{\theta})=\dot{\theta}\hat{\theta}##
##\frac{d\vec{r}}{dt}=\frac{dr}{dt}\hat{r}+r\frac{d\hat{r}}{dt}=\frac{dr}{dt}\hat{r}+r\dot{\theta}\hat{\theta}##
This is the first method. The second method is more complex than the first one as my opinion.
Let me show you the second method,
As ##\hat{r}## and ##\hat{\theta}## unit vectors are defined on a circle, to understand them and their derivation over time we have to examine a particle's motion along a circle. In circular motion, at ##\Delta t## time the ##\hat{r}## unit vector becomes ##\hat{r}+\Delta \hat{r}##. When ##\Delta t\to 0##, ##\Delta \hat{r}## and ##\hat{\theta}## are in the same direction (Fig. 2.20a, 2.20b). If ##\Delta \theta \to 0## next to ##\Delta t##, the magnitude of ##\Delta \hat{r}##,

##\left|\Delta \hat{r}\right|=\left|\hat{r}\right|\Delta \theta=\Delta \theta##
Because ##\left|\hat{r}\right|=1##. So,
##\Delta \hat{r}=\Delta \theta\hat{\theta}##
[Q-1: Here, how this equation is possible to equal? Because ##\Delta \theta## is a radian or degree and what does mean it's multiplication with ##\hat{\theta}## unit vector? A figure, schema, graph or example would be fine!]
[Q-2: Also, when we multiply the both sides of ##\left|\Delta \hat{r}\right|=\left|\hat{r}\right|\Delta \theta=\Delta \theta## with ##\hat{\theta}## how we get ##\Delta \hat{r}=\Delta \theta\hat{\theta}##?]
##\frac{\Delta\hat{r}}{\Delta t}=\frac{\Delta \theta}{\Delta t}\hat{\theta}##
[Q-3: Here, we divide both sides with ##\Delta t## but on the right side we have ##\frac{\Delta \theta}{\Delta t}\hat{\theta}## instead of ##\frac{\Delta \theta\hat{\theta}}{\Delta t}##, because the ##\hat{\theta}## is changing by time and it can be rewrited as a function of time (t) ##\hat{\theta}(t)##. We haven't touched ##\hat{\theta}## on the equation althogh it's changing by time. Why?]
In ##\Delta t\to 0## limit case, we get the following result
##\frac{d\hat{r}}{dt}=\frac{d\theta}{dt}\hat{\theta}##
With the smilar processes, we get ##\frac{d\hat{\theta}}{dt}=-\frac{d\theta}{dt}\hat{r}##. This process is related with the given figure below (Fig. 2.20c).
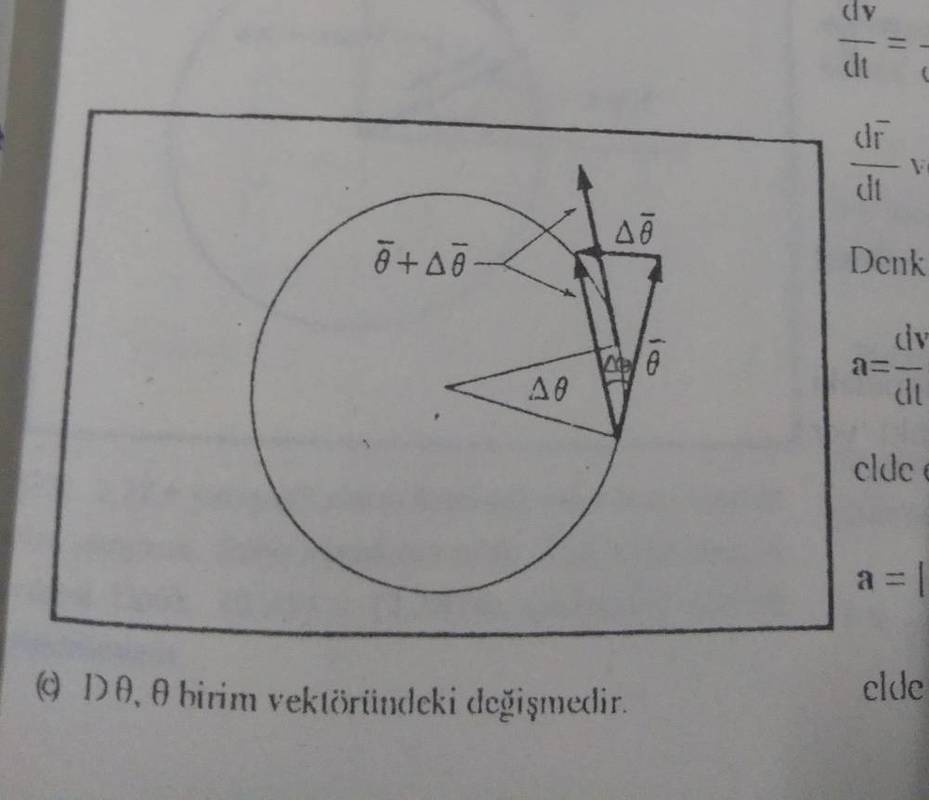
And lastly, if we put the ##\frac{d\hat{r}}{dt}## and ##\frac{d\hat{\theta}}{dt}## into the velocity vector formula, we get
##\vec{V}=\frac{d\vec{r}}{dt}=\frac{d}{dt}(r(t)\hat{r}(t))=\frac{dr}{dt}\hat{r}+r\frac{d\hat{r}}{dt}##
##\vec{V}=\frac{dr}{dt}\hat{r}+r\frac{d\theta}{dt}\hat{\theta}##
That's it!
Thanks!
##\vec{V}=\frac{d\vec{r}}{dt}=\frac{dx}{dt}\hat{x}+\frac{dy}{dt}\hat{y}+\frac{dz}{dt}\hat{z}##
in Cartesian Coordinate Systems ##(x, y, z)##. I want to convert this into Polar Coordinate System ##(r, \theta)##.
##\vec{r}=r(t)\hat{r}(t)##
##\frac{\vec{r}}{dt}=\frac{d}{dt}[r(t)\hat{r}(t)]=\frac{dr}{dt}\hat{r}+r\frac{d\hat{r}}{dt}##
There are 2 methods to get velocity vector formula that is defined on Polar Coordinate Systems.
First method is like this,
##\hat{r}=\hat{x}\cos{\theta}+\hat{y}\sin{\theta}##
##\hat{\theta}=-\hat{x}\sin{\theta}+\hat{y}\cos{\theta}##
##\frac{d\hat{r}}{dt}=-\sin{\theta}\dot{\theta}\hat{x}+\cos{\theta}\dot{\theta}\hat{y}##
##\frac{d\hat{r}}{dt}=\dot{\theta}(-\sin{\theta}\hat{x}+\cos{\theta}\hat{y})##
##\frac{d\hat{r}}{dt}=\dot{\theta}(\hat{\theta})=\dot{\theta}\hat{\theta}##
##\frac{d\vec{r}}{dt}=\frac{dr}{dt}\hat{r}+r\frac{d\hat{r}}{dt}=\frac{dr}{dt}\hat{r}+r\dot{\theta}\hat{\theta}##
This is the first method. The second method is more complex than the first one as my opinion.
Let me show you the second method,
As ##\hat{r}## and ##\hat{\theta}## unit vectors are defined on a circle, to understand them and their derivation over time we have to examine a particle's motion along a circle. In circular motion, at ##\Delta t## time the ##\hat{r}## unit vector becomes ##\hat{r}+\Delta \hat{r}##. When ##\Delta t\to 0##, ##\Delta \hat{r}## and ##\hat{\theta}## are in the same direction (Fig. 2.20a, 2.20b). If ##\Delta \theta \to 0## next to ##\Delta t##, the magnitude of ##\Delta \hat{r}##,
##\left|\Delta \hat{r}\right|=\left|\hat{r}\right|\Delta \theta=\Delta \theta##
Because ##\left|\hat{r}\right|=1##. So,
##\Delta \hat{r}=\Delta \theta\hat{\theta}##
[Q-1: Here, how this equation is possible to equal? Because ##\Delta \theta## is a radian or degree and what does mean it's multiplication with ##\hat{\theta}## unit vector? A figure, schema, graph or example would be fine!]
[Q-2: Also, when we multiply the both sides of ##\left|\Delta \hat{r}\right|=\left|\hat{r}\right|\Delta \theta=\Delta \theta## with ##\hat{\theta}## how we get ##\Delta \hat{r}=\Delta \theta\hat{\theta}##?]
##\frac{\Delta\hat{r}}{\Delta t}=\frac{\Delta \theta}{\Delta t}\hat{\theta}##
[Q-3: Here, we divide both sides with ##\Delta t## but on the right side we have ##\frac{\Delta \theta}{\Delta t}\hat{\theta}## instead of ##\frac{\Delta \theta\hat{\theta}}{\Delta t}##, because the ##\hat{\theta}## is changing by time and it can be rewrited as a function of time (t) ##\hat{\theta}(t)##. We haven't touched ##\hat{\theta}## on the equation althogh it's changing by time. Why?]
In ##\Delta t\to 0## limit case, we get the following result
##\frac{d\hat{r}}{dt}=\frac{d\theta}{dt}\hat{\theta}##
With the smilar processes, we get ##\frac{d\hat{\theta}}{dt}=-\frac{d\theta}{dt}\hat{r}##. This process is related with the given figure below (Fig. 2.20c).
And lastly, if we put the ##\frac{d\hat{r}}{dt}## and ##\frac{d\hat{\theta}}{dt}## into the velocity vector formula, we get
##\vec{V}=\frac{d\vec{r}}{dt}=\frac{d}{dt}(r(t)\hat{r}(t))=\frac{dr}{dt}\hat{r}+r\frac{d\hat{r}}{dt}##
##\vec{V}=\frac{dr}{dt}\hat{r}+r\frac{d\theta}{dt}\hat{\theta}##
That's it!
Thanks!
Last edited: