kent davidge
- 931
- 56
I want to show some of my current understanding/findings involving vector spaces. The reason is two fold: to ask whether my current understanding is ok and to give context for a specific question in the end.
The set ##\{(x,0), (0,y) \}##, with ##x,y \in \mathbb{R}##, spans ##\mathbb{R}^2##. For example, ##\{(1,0), (0,1) \}## is the canonical basis.
It's clear that a vector will remain the same under a change of basis. For instance, consider a vector having components ##a,b## in the basis ##\{(2,0),(0,3) \}##, i.e. ##a(2,0) + b(0,3)##. It naturally will be ##2a(1,0) + 3b(0,1)## in the canonical basis, but it's the same vector in ##\mathbb{R}^2##.
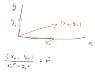
Now consider ##x = r \cos \theta, y = r \sin \theta##, with ##r, \theta \in \mathbb{R}##, the so called polar coordinates. It also spans ##\mathbb{R}^2##. By the above reasoning regarding the basis, for each pair ##(r, \theta)## (not both equal to zero) we have a different basis for ##\mathbb{R}^2##.
The problem I see is that people do not typically writes a vector like ##a(r \cos \theta, 0) + b(0, r \sin \theta)##. So this make me suspicious that my way of doing it is not correct.
Also, following the presented reasoning, if we want the measures of distances (yea, I should have said metric) to be the same in the two given basis, I found that we need to do the following.
Evaluate ##dx## and ##dy## at ##\theta = 0## to get ##\{(dr, 0), (0, r d \theta) \}##. Then ##dx^2 + dy^2 = dr^2 + r^2 d \theta^2##. The question that arises is why this would happen exactly if ##\theta = 0##.
The set ##\{(x,0), (0,y) \}##, with ##x,y \in \mathbb{R}##, spans ##\mathbb{R}^2##. For example, ##\{(1,0), (0,1) \}## is the canonical basis.
It's clear that a vector will remain the same under a change of basis. For instance, consider a vector having components ##a,b## in the basis ##\{(2,0),(0,3) \}##, i.e. ##a(2,0) + b(0,3)##. It naturally will be ##2a(1,0) + 3b(0,1)## in the canonical basis, but it's the same vector in ##\mathbb{R}^2##.
Now consider ##x = r \cos \theta, y = r \sin \theta##, with ##r, \theta \in \mathbb{R}##, the so called polar coordinates. It also spans ##\mathbb{R}^2##. By the above reasoning regarding the basis, for each pair ##(r, \theta)## (not both equal to zero) we have a different basis for ##\mathbb{R}^2##.
The problem I see is that people do not typically writes a vector like ##a(r \cos \theta, 0) + b(0, r \sin \theta)##. So this make me suspicious that my way of doing it is not correct.
Also, following the presented reasoning, if we want the measures of distances (yea, I should have said metric) to be the same in the two given basis, I found that we need to do the following.
Evaluate ##dx## and ##dy## at ##\theta = 0## to get ##\{(dr, 0), (0, r d \theta) \}##. Then ##dx^2 + dy^2 = dr^2 + r^2 d \theta^2##. The question that arises is why this would happen exactly if ##\theta = 0##.
 I did ! But, like a genuine ass, I only did it once: in #4 I write that ##\hat r## and ##\hat\theta## are perpendicular
I did ! But, like a genuine ass, I only did it once: in #4 I write that ##\hat r## and ##\hat\theta## are perpendicular