Cosmo calculators with tabular output

[marcus]

Hi Jorrie, I just saw your edit. I think you are right that the curve physically stops at 16.3 where the time for the signal to reach target goes to infinity. If it takes an infinite time for a our signal to reach a galaxy at 16.3 Gly that clearly says it is the limit. I like the clarity.

Can't think of any physical meaning of negative stretch, or negative scale factor.

To me it looks like the calculator does what it has to do, what it should do. reach the axis (where time=) exactly at the right place. It's a really satisfying gadget, you must be be having some proud papa moments these days.

(Or so it seems to me---as a non-expert interested in the subject.)

btw I like the "down-step" feature! It let's me get the size table I want without having to calculate what the step size should be to achieve that. And when I change the upper and lower limits of the table, it stays the desired size. Good (though unconventional) use of the minus sign

EDIT: Hi Jorrie, just saw your next post which wakes me up to the fact that I should have been saying 15.6 here instead of 16.3. The y-intercept of the D_now curve should give the present value of the cosmic event horizon (which is around 15.6 Gly) not the future value.

Here are nice graphs of most of those columns:

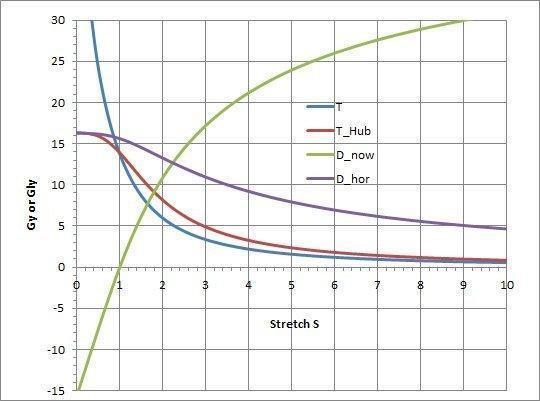
Edit:
The "y-intercept" of the green curve is in fact just an artefact of this thread's definition of D_now for the future: the (negative) distance to an observer that will receive our present signals with a stretch 1/S, i.e. with redshift 1/S + 1. The y-intercept represents the cosmic even horizon (16.3 Gy), where redshift (and time to reach) tends to infinity. Negative S does not have a physical meaning, or does it? One can mathematically extend the curve to the negative domain, but I have no idea what it may mean.

 

[Jorrie]

... I have a suspicion that D_now is not correct for the future (S < 1), because I think it is supposed to asymptotically approach the S = 0 line, while it appears to be heading for an intercept. ...

I was wrong; it is actually the future D_then value that diverges to negative infinity, as is clear from this chart.

One can also see the position of the 'equator' of the usual 'teardrop' (or 'onion') shape, where T_Hub and D_then cross over (S = 2.64). This is the maximum value of D_then for all of time (given the standard model and values).

...
Edit:
The "y-intercept" of the green curve is in fact just an artefact of this thread's definition of D_now for the future: the (negative) distance to an observer that will receive our present signals with a stretch 1/S, i.e. with redshift 1/S + 1. The y-intercept represents the cosmic even horizon (16.3 Gy), where redshift (and time to reach) tends to infinity.
...

Wrong again; must have been weekend laziness...

The "y-intercept" of the green curve represents (the negative of) the distance to our or present cosmic event horizon (CEH), at 15.6 Gly. An observer presently at that proper distance will never receive our present signals (and neither will we receive theirs). If accelerated expansion continues as we expect, our future CEH will only reach 16.3 Gly by around 74 Gy from now.

 

[marcus]

That's an especially nice chart with the 5 curves (time=black, horizon=sky blue, ...etc).
I like being able to spot the equatorial bulge on the onionshape lightcone by where the red and purple curves cross, at S=2.64.

Your post alerts me to my having misspoke in post#31, the current CEH being 15.6, I should have been saying that instead of the longterm CEH value of 16.3. The presentday D_now curve should have a y-intercept at the presentday CEH, so at or around -15.6. Which (allowing for the limitations of finite accuracy) it does seem to do!

 

[Jorrie]

Since there may be a change in the generally accepted values for H₀ and Omega_m coming (http://arxiv.org/abs/1208.3281%22), and it may change values for i.a. Cosmic time (age) and Lookback time, I have included Lookback time in the list of compact equations that was listed before.

Given present Hubble time Y_{now}, long term Hubble time Y_{inf} and the redshift for radiation/matter equality z_{eq}. Since the factor z + 1 occurs so often, an extra parameter S = z + 1 = 1/a is defined, making the equations neater.

\Omega_\Lambda = \left(\frac{Y_{now}}{Y_{inf}}\right)^2, \ \ \, <br /> \Omega_r = \frac{1-\Omega_\Lambda}{1+S_{eq}}, \ \ \,<br /> \Omega_m = S_{eq}\Omega_r

Hubble parameter
H = H_0 \sqrt{\Omega_\Lambda + \Omega_m S^3 (1+S/S_{eq})}

Hubble time, Cosmic time , Lookback time T_look added
Y = 1/H, \ \ \, <br /> T = \int_{S}^{\infty}{\frac{dS}{S H}}, \ \ \,<br /> T_{look} = \int_{1}^{S}{\frac{dS}{S H}}
Proper distance 'now', 'then' and cosmic event horizon
D_{now} = \int_{1}^{S}{\frac{dS}{H}}, \ \ \, <br /> D_{then} = \frac{D_{now}}{S}, \ \ \, <br /> D_{CEH} = \frac{1}{S} \int_{0}^{S}{\frac{dS}{H}}

This essentially means integration for S from zero to infinity, but practically it has been limited to 10^{-7} &lt; S &lt; 10^{7} with quasi-logarithmic step sizes, e.g. a small % increase between integration steps.

Using the quoted H₀ = 74.3 km s^-1 Mpc^-1 and Omega_m = 0.278, a rerun of the above numerical integrations gives:

Hubble times: Y_now = 13.3 Gyr, Y_inf = 15.5 Gyr, T_now = 12.96 Gyr and the lookback time to the current most distant galaxy T_z=9.6 = 12.54 Gyr.

Since the change in Omega_m was small, the times essentially changed by the ratio H₀(old)/H₀(new), but this will not hold if Omega_m changes significantly, or the deviation from spatial flatness is significant.

 

[Jorrie]

For anyone who missed the discussion in Marcus' "88 billion year" sticky above, here is the latest version of the "inhouse" tabular cosmo-calculator, as also shown in Marcus' signature (TabCosmo5.html).

The main changes since September last year are: an easy method to get a logarithmic spread of redshifts (actually stretch S = z+1) and that the latest (2013) WMAP9 (combined) maximum likelihood parameters are now used. Please read the info tool-tips of the calculator for clarification of usage.

Here is a sample plot of data generated by the calculator, as copied into a spreadsheet.

Of particular interest from the visuals are the following observations:

1. The max value of D_then ~ 5.8, where D_then crosses T_Hub at S ~ 2.62. You will need 29 S-steps to spot this max precisely on a generated table.
   
2. The correspondence of T_Hubble and D_hor when S < ~0.3, where the cosmological constant completely dominates.
   
3. The 'straight' T-curve into the future (S < 1), with an equation T \approx 13 - 16.5 \ln(S) Gy, with 13 roughly the y-intercept of the linear portion and 16.5 is Y_inf (Hubble time in far future).

 

[marcus]

Part of what Jorrie was just talking about. I.e. stretch factor 2.63 and emission distance 5.8, has to do with the beautiful fact that past lightcones are TEAR-DROP SHAPE.

You can see that at the top level of the "figure 1" in my signature. That is what they look like when you measure in proper distance, the real distance that it actually was at the time, if you could have stopped the expansion process.

Other levels of the "figure 1" show conformal distance---what the distance to that same bit of matter would be today, not what it was back then. So the lightcone is not teardrop, it is some other shape.

the point of S=2.63 is that where the WIDEST bulge of the teardrop comes, in our past light cone. The largest girth. Farther back in time from then, the light cone PULLS IN. Of course that's because distances were smaller back then---and it is what gives it the teardrop or pear shape.

A rather beautiful thing happened around S=2.63 namely when galaxies emitted light then, that was destined to get here today for us to receive with telescopes, that light stayed at the same distance from us for a long time. Making barely if any progress. It stayed at distance 5.8, or more precisely according to the calculator, 5.798. Because its forward motion thru the surrounding space exactly canceled the rate at which the distance 5.798 was growing! So no net headway!

And then after a long time that distance 5.798 had slowed slightly and was not growing at the speed of light and the photons began to make headway towards us. The calculator will give an idea how long they took, all told, to get here. I think it was very nearly 10 billion years.

So you see in the preceding post Jorrie suggests putting 29 into the STEPS box, and also be sure to check the "exactly S=1" box so you get the exact present in your table. Then you will get, among much else, the S=2.62 line in the table, and that 5.8, and the time, what year it was etc.

The widest girth is at a crossing point in the figure which basically says the distance was growing at exactly c. You can see where the two curves cross. Blue and green. Blue for the emission distance, green for the Hubble distance (that distance which is growing at speed c.)

If you click on figure 1 in my signature you will also see a crossing of curves that marks this widest point on the teardrop lightcone. (In the top layer, the version drawn using proper distance. Other layers distort shape.)

 

[Jorrie]

... stretch factor 2.63 and emission distance 5.8, has to do with the beautiful fact that past lightcones are TEAR-DROP SHAPE.

You can see that at the top level of the "figure 1" in my signature. That is what they look like when you measure in proper distance, the real distance that it actually was at the time, if you could have stopped the expansion process.

I have massaged a spreadsheet of the tabular data a little in order to plot a graph that looks somewhat like the top level Davis plot in your sig. In the process I became interested in the relationship between the event horizon and the particle horizon and subsequently have added a column for the particle horizon to TabCosmo5 (saved as TabCosmo6). Graphically it looks like this:

It corresponds (partially) to the Davis diagram turned on its side, with the 'teardrop' the two opposite side D_then distances, crossing and diverging in the future.

Interestingly, there are two other intersections happening simultaneously at another cosmic time, T~4 Gy: (i) the Hubble sphere crossing the past light cone and (ii) the event horizon crossing the particle horizon.

Crossing (i) is as you explained in your prior post, but I'm not sure why crossing (ii) happens at the same time (or at least very closely so, as far as I can tell). The correspondence seems to be independent of the choice of input parameters (Ynow and Yinf).

If I have it right, the cosmic event horizon is the largest proper distance (at time of emission) between an emitter and receiver that light can ever bridge, while the particle horizon is the proper radius of the observable universe at the time of the emission of the signal that is observed at stretch S.

Is it because observed redshift at the event horizon will tend to infinity?

 

[marcus]

Nice!
The present moment is shown in an elegant graphic way as the point joining the past and future lightcones. I'll think about your question shortly, just wanted to respond immediately to the figure

 

[marcus]

Sorry, I got dragged off to lunch and had to prune trees in the garden. I see that simultaneous intersection clearly! I can't explain it. I'll keep thinking about it and may have some luck later.

 

[Chronos]

That is my understanding too, Jorrie. The redshift approaches infinity by the time photons currently emited at the CEH reach us. Of course, the time it takes those photons to reach us also approaches infinity. If you think in terms of scale factor, it all seems to make sense.

 

[marcus]

One thing that occurs to me is that Lineweaver is a talented explainer who devoted his lifetime to cosmology and his figure 1 has THREE bands. Probably you can't get the whole thing into one picture and if you try to, the first picture will start getting complicated and won't communicate as well.

The THIRD band of figure 1 uses comoving distance (each bit of matter is given an unchanging label) and the timescale is adjusted to match that. Then particle horizon is a straight 45 degree line that intersects event horizon which is also a straight 45 degree line and is effectively "the past lightcone at infinity".

The story you can tell about that intersection (P horizon with E horizon) is of a RADAR ECHO. We send out a PING at the start of expansion, and we ask what is the most distant matter that can echo back or send a reply message to us, that we would eventually receive if we could wait arbitrarily long. If we could wait "till infinity" to hear the reply or the echo, then what is the most distant matter we could contact that way. With the whole history of the universal expansion to do it in, to make contact.

And I think your tabular calculator gives the answer to that, and it says WHEN the radar signal bounces, if I recall it is around year 4 billion, which is when the lines intersect. I have to check this.

Yes, I'm just using version 5. It says that the proper distance to that farthest ever ping-able matter is 11.8 Gly, that is at the moment it gets our message (we sent at the start of expansion) and echos it back. And that is at S=2.63. So to find the distance NOW I have to multiply 11.8*2.63 = 31 Gly
And distance now of some particular bit of matter is what they call its "comoving" distance. So that 31 Gly should agree with Lineweaver figure 1.

Actually I don't think this has to do with infinitely redshifting light. It is not what you can practically get a radar ping from it is what you can do IN PRINCIPLE. using arbitrarily large antennas and arbitrarily sensitive receivers etc etc. Let me check and see if Lineweaver puts that intersection at 31 Gly.

Yes, bingo! right on 31 Gly! So I think the analysis is all right.

Now there is still the puzzle Jorrie posed which is why that farthest matter echo event happens right at S = 2.63.
Why should it coincide with...? Have to think some more about that. If somebody else doesn't come up with an explanation I'll think about it tomorrow morning when I'm fresh. We're only just getting started on that one, I think. Intriguing coincidence!

 

[marcus]

This is strange. Using the new calculator version6, I don't actually get a coincidence.
I'm putting in Step=0 so I just get a one-line table, for S=2.632
That is what I am used to using to get the intersection of Hubbleradius and D_then. Or even better: S=2.6321

But that does not give a match between D_hor and particle horizon D_par! It looked on the figure as if they were at the same level so I thought there was an exact coincidence (but couldn't figure out why there would be) and now the table does not give a coincidence.

11.804 ≠ 11.934

Am I missing something? being really dense? Sorry for a possible bungling lapse of competence. Can someone explain this almost but not quite coincidence?

To get D_hor to equal D_par, you have to go to S=2.662
11.736 ≈ 11.735

well, let's still find the comoving (now) distance to the farthest pingable matter: 2.662*11.735 = 31.2 Gly. Yes! that's still good.

I suppose that twice that, namely 62.4 Gly is the distance now of the farthest matter we will ever hear from regardless how long we wait.

 

[Jorrie]

But that does not give a match between D_hor and particle horizon D_par! It looked on the figure as if they were at the same level so I thought there was an exact coincidence (but couldn't figure out why there would be) and now the table does not give a coincidence.

11.804 ≠ 11.934

Am I missing something? being really dense? Sorry for a possible bungling lapse of competence. Can someone explain this almost but not quite coincidence?

To get D_hor to equal D_par, you have to go to S=2.662
11.736 ≈ 11.735

I have also noticed this, but my first reaction was that it is caused by small errors in the numerical integration loops of the various curves. Remember that to get all the values perfect, it requires integration for time (or S) from zero to infinity with an 'infinite number of steps', which is not feasible. Especially D_hor is very susceptible to cut-off errors.

What is intriguing is that the rough correspondence remains when Ynow and Yinf are changed. I'm busy looking at it analytically (not easy) and will report what I find.

 

[marcus]

Because you are doing hard analytical work I should probably be quiet and not distract from that. I had something else I wanted to say, though. It seems to me that the distance 11.735 Gly is somehow UNIVERSAL. It does not know about us, that we are in year 13.7 Gy or so. It depends on sending out a radar ping at the start of the expansion, from wherever you are, and then being able to wait to year infinity to hear back.

The farthest distance, as a proper distance from your matter when the bounceback happens, should be the same for anyone in the universe at any stage in its history.

Is the distance 5.8 comparably universal? It seems strange that it should be roughly HALF of 11.735

But that could be a spurious coincidence. I dimly suspect that the distance 5.8 depends on WHEN in the history of the universe you are. It is the maximum proper distance at emission-time of any light we can detect now. I may be missing something, but that seems to depend on when in the history of the universe we are.

 

[Jorrie]

The redshift approaches infinity by the time photons currently emited at the CEH reach us. Of course, the time it takes those photons to reach us also approaches infinity. If you think in terms of scale factor, it all seems to make sense.

Yes, it is a bit clearer in terms of scale a = 1/S and comoving distances. Working on that.
From Davis http://arxiv.org/abs/astro-ph/0402278 (2004), Eqs. A.19 and A.20, pp. 117, with c=1:

\chi_{par}= \int_{0}^{t}{ \frac{dt}{a}} = \int_{0}^{a}{ \frac{da}{a^2 H}}
\chi_{hor} = \int_{t}^{\infty}{ \frac{dt}{a}} = \int_a^\infty { \frac{da}{a^2 H}}

where H = H_0 \sqrt{\Omega_\Lambda + \Omega_m S^3 (1+S/S_{eq})} and S = 1/a = 1+z (post #34 above). Further from #34, written in comoving form:

\chi_{Hub}= \frac{1}{a H}
\chi_{then} = \int_{1}^{S}{ \frac{dS}{H}} = \int_a^1 { \frac{da}{a^2 H}}

This looks deceptively easy, but since H is a function of a, I have no idea how to analytically solve for a for either of the two crossings. Maybe Maple software can help? (I do not have it).

Anyone with ideas?

 

[marcus]

...Anyone with ideas?

This is not the type of idea you specifically asked for, but let's explore the idea that the apparent coincidence may be spurious. If that's wrong, and it is a mathematical equality some reader will show up, I trust, and explain. Meanwhile I make the tentative assertion that the maximum girth of the teardrop lightcone (and the time that occurs) depends strongly on where we are in the history of the universe. If we were later the teardrop would be bigger and the bulge would come later. We wouldn't be seeing that time figure of 4 Gy and that maximum emission distance figure of 5.8 Gly. If we were earlier/later in the expansion process those numbers would each be smaller/larger.

So if you want to destroy the spurious coincidence (I assert tentatively) then you don't change the parameters of the universe, you should figure out what numbers we will see later on, or would have seen earlier. Construct our perspective for some time in future.

Because I think the maximum proper distance of a radar bounce is a universal INVARIANT, and so is the year that bounce occurs. It is going to be the same as long as the basic cosmic parameters are the same, whether from the perspective of some one earlier than us or someone far in the future. the reason is that the present expansion age does not enter into the definition.

The greatest proper distance of a radar bounce is always going to be 11.735 Gly and the time that bounce occurs is always going to be year 4 billion. Or 3.97...something billion, to be finicky.

The definition is you imagine sending out a signal right at the start of expansion. And every time it hits something part of the signal bounces back. And at first all those return echos are destined to get back to us eventually. If we wait long enough we will hear the ping.

But there comes a time (year 3.97... billion ) when the signal is at a proper distance of 11.735 Gly, and it makes its LAST BOUNCE that is ever destined to get back to us. Because it has reached a "point of no return", which is the event horizon.

When the particle horizon curve meets the event horizon curve there is no more pingback return from then on. The signal makes the last bounce we can expect to hear.

I'll think about this some more, but it seems obviously independent of when in the expansion history we happen to be at the present time. (which I expect the other numbers aren't independent of, so the coincidence has to be fortuitous even though bizarrely close.)

 

[marcus]

I checked. The coincidence does see merely accidental. I used version 6 and put in S_lower = 1 and Steps=50 (to get nice resolution).

Then I put in Y_now = 12.0 instead of 14.0. That corresponds to an earlier time in the same universe. The age is now only around 10 Gy instead of 13.7 Gy.

Then I looked down to where the TIME was about 3.99 Gy which is when we expect the farthest radar bounce to occur and in fact it did! Both Dhor and Dpar were around 11.7 and roughly equal.

But at that moment in time the other two numbers were NOT roughly equal. Dthen was nowhere near Thub. So people living in Milkyway back in year 10.14 billion would NOT see the coincidence we are talking about.

their maximum teardrop bulge would have occurred around year 2.9 billion and their max pingback bounce would have occurred (as it always does in our universe) at year 4 billion or so.

I didn't bother to adjust the 3250 number for the different perspective because I don't think it would have made any great difference.

I must say I like version 6! Will have to change link in signature.

 

[George Jones]

I checked. The coincidence does see merely accidental.

Here's another way (or the same way from a slightly different perspective) to see this.

The particle and event horizons do not depend on a "now" event, so their intersection does not depend on a "now" event. The Hubble sphere does not depend on "now", but the past lightcone does depend on "now", so their intersection does depend on "now". This is particularly evident in Figure 1 from Davis Lineweaver. As the "now" line shifts up and down, the intersection of the past lightcone and the Hubble sphere changes (for me, especially clear in the bottom panel), but the intersection of the particle and event horizons remains the same.

 

[marcus]

Here's another way (or the same way from a slightly different perspective) to see this.

The particle and event horizons do not depend on a "now" event, so their intersection does not depend on a "now" event. The Hubble sphere does not depend on "now", but the past lightcone does depend on "now", so their intersection does depend on "now". This is particularly evident in Figure 1 from Davis Lineweaver. As the "now" line shifts up and down, the intersection of the past lightcone and the Hubble sphere changes (for me, especially clear in the bottom panel), but the intersection of the particle and event horizons remains the same.

Good! Clear concise way to explain it. Thanks, George.

 

[Jorrie]

This is particularly evident in Figure 1 from Davis Lineweaver. As the "now" line shifts up and down, the intersection of the past lightcone and the Hubble sphere changes (for me, especially clear in the bottom panel), but the intersection of the particle and event horizons remains the same.

Thanks, this gives a clear picture. Like Marcus, I could not find any further empirical or analytical evidence anyway.

 

[Jorrie]

I checked. The coincidence does seem merely accidental. I used version 6 and put in S_lower = 1 and Steps=50 (to get nice resolution).

Then I put in Y_now = 12.0 instead of 14.0. That corresponds to an earlier time in the same universe. The age is now only around 10 Gy instead of 13.7 Gy.

My first reaction was that only the Ynow change would not give valid calculation for an earlier epoch, but to my surprise it works as you have done it. Leaving all the other stuff the same, the calculator calculates the new earlier energy balance and in effect just shrinks the past light cone, while the other outputs remain the same. It essentially just shifts the now-line up and down on the Davis Figure 1. Its a new usage of the tool that you have discovered. :-)

It's bed time in my valley, so I will look at it again some time tomorrow.

 

[Jorrie]

My first reaction was that only the Ynow change would not give valid calculation for an earlier epoch, but to my surprise it works as you have done it. Leaving all the other stuff the same, the calculator calculates the new earlier energy balance and in effect just shrinks the past light cone, while the other outputs remain the same. It essentially just shifts the now-line up and down on the Davis Figure 1. Its a new usage of the tool that you have discovered. :-)

I am no longer so sure that this is valid. Although it shifts the now-line up and down, it also changes the convergence on 62.3 Gly (comoving) to some 47.5 Gly. I have checked this convergence on a spreadsheet with Marcus' Y_now = 12 example, leaving the rest the same. This does not seem right. Since D_comoving = S D_proper, and we use the same S, one would expect the 62.3 to stay the same (?). The calculator is designed to work for inputs as at present and it assumes that changing the inputs change the present observed parameters. The past and present values should only be read off the table (or graphs of it).

Since the original Davis graphs are so much clearer, I have converted the complete diagram to .jpg and attached it. Since it is now on resident on PF, maybe you should change the link in your sig to this one. It remains pretty clear when zoomed in by means of a browser.

 

[marcus]

Hi Jorrie, I neglected to mention something earlier because it wasn't essential to finding proper distances (in the lightcone of someone back in year 10.15 billion).

Their comoving distances are reduced by a factor of 1.318.

Because their stretch factors are all reduced by a factor of 1.318. They see recombination (the origin of the CMB) as having occurred not at stretch 1090 but at 1090/1.318.

I mentioned earlier I think that I hadn't bothered to change S_eq (because it doesn't make much difference) but that event would have occurred at 3280/1.318 = 2489.
So to be more careful, if you want to use your version 6 as a "time machine" then to go back to year 10.15 billion you should put in

12.0 instead of 14.0
2489 instead of 3280 (but that makes very little difference so for a quick and dirty we don't need to change S_eq)

I will explain this some more but wanted to send you this right away.

 

[marcus]

What you found a couple of posts back was quite consistent. Try dividing our comoving distance 62.3 by the factor 1.318. It should give approximately the right thing.

The basic time machine experiment we did was to change the Hubbletime (Ynow) from 14.0 to 12.0 and that jumps us back into essentially the same universe but at year 10.148 or call it 10.15 billion.

But when we go back then, distances are all less by a factor of 1.318. You can check that by staying in our timeframe (Ynow=14.0) and putting in S=1.318 and you will get that Time=10.15 billion.

So we know that in our universe, if we go back to year 10.15 billion distances (in that year) are less by that factor. We don't have to worry about that if we are just talking about PROPER distance because that has a kind of independent meaning regardless of what year we are living in. But comoving distances, which are "now" distances at the time we are living in, will be different because we are in a different present. So we have to adjust the S values accordingly and the comoving distances.

I could always be wrong about this but I'm pretty sure in this instance that it is right.

It's a great calculator! We keep finding more things one can do with it. I suspect that it's an idea whose time is come and we are apt to see other tabular cosmic calculators appear in the next 2 or 3 years. This one will plant a seed in some people's minds and they will talk to other people who talk with other people. And then someone will get the idea and not know where he got it from. the idea will be "in the air". That's how I think it is apt to go. The universe is about continuity and development, so tabular output is natural to it.

Thanks for finding the Tamara Davis originals. They are sharp, and color-coded. I think maybe both Davis and Lineweaver are talented communicators (as well as first-rate cosmologists).
I suspect Lineweaver saw a good thing when his Phd student Davis showed him that 3-layer "figure 1" and he adopted it straight off the bat. Science progresses not only by people discovering things but also by their finding really good ways to transmit the important ideas. (Or so I think---just my two cents as an onlooker.)

 

[Jorrie]

What you found a couple of posts back was quite consistent. Try dividing our comoving distance 62.3 by the factor 1.318. It should give approximately the right thing.

Yes, I think you are quite right :) Past and future observers would 'freeze frame' the expansion at different stages than us and hence their equivalent definition of comoving distances would yield different values for the same objects/horizons.

It is very interesting that the new Ynow input automatically adjust Ho, Ω_λ and Ω_m. This is an advantage over the usual Ho and Ω input calculators, which usually can take a combination that is invalid (without user knowing it). I must look at a way to adjust S_eq and S_CMB defaults automatically as well and it will be even more convenient for all sorts of cosmo calculations. One can obviously override any of them manually if you want...

 

[marcus]

I must look at a way to adjust S_eq and S_CMB defaults automatically as well and it will be even more convenient for all sorts of cosmo calculations. One can obviously override any of them manually if you want...

An alternative might be to SUGGEST over on the right what S_CMB the user might like to use, and expect him to type in something different from 1090. For me, it was a learning experience to have to put different stuff in the boxes. A mild "learn by doing" experience, not earth-shaking. But I sense the value of having to do something myself now and then, to get an interesting effect, rather than having the calculator always do it for me.

Basically however, I trust your pedagogical machine design sense. So far all your added features seem like definite improvements and not "too much". It's become a really fine learning machine---someone could write a brief user manual which would suggest things to do with it---cosmological exercise book, things to try on it.

I wish I knew someone who was teaching Introduction to Cosmology at some college or university. I'd like to see TabCosmo tried out for use in a class. I know OF people but I'm not in close enough personal touch with the right ones to be effective.

Does anybody here know of someone teaching Astronomy for Non-Majors or something comparable?

 

[Jorrie]

An alternative might be to SUGGEST over on the right what S_CMB the user might like to use, and expect him to type in something different from 1090.

It appears simple, but it turns out to be a rather involved programming change, so it must go to the back burner for now. I will include the steps that you have used somewhere in the info tips in a future update. They are simple enough and as you said, serve some educational purpose. Good work, Marcus.

 

[Jorrie]

For completeness of reference,^[1] here is the full compact set of TabCosmo6 equations (added particle horizon from previous).
Given present Hubble time Y_{now}, long term Hubble time Y_{inf} and the redshift for radiation/matter equality z_{eq}
Since the factor z + 1 occurs so often, an extra parameter S = z + 1 = 1/a is defined, making the equations neater.
\Omega_\Lambda = \left(\frac{Y_{now}}{Y_{inf}}\right)^2, \ \ \, <br /> \Omega_r = \frac{1-\Omega_\Lambda}{1+S_{eq}}, \ \ \,<br /> \Omega_m = S_{eq}\Omega_r
Hubble parameter, also referred to as H(t)
H = H_0 \sqrt{\Omega_\Lambda + \Omega_m S^3 (1+S/S_{eq})}
Hubble time, Cosmic time
Y = 1/H, \ \ \, <br /> T = \int_{S}^{\infty}{\frac{dS}{S H}}
Proper distance 'now', 'then', cosmic event horizon and particle horizon
D_{now} = \int_{1}^{S}{\frac{dS}{H}}, \ \ \, <br /> D_{then} = \frac{D_{now}}{S}, \ \ \, <br /> D_{CEH} = \frac{1}{S} \int_{0}^{S}{\frac{dS}{H}}, \ \ \,<br /> D_{par} = \frac{1}{S}\int_{S}^{\infty}{ \frac{dS}{H}}<br />
To obtain all the values, it essentially means integration for S from zero to infinity, but practically it has been limited to 10^{-7}&lt; S &lt;10^{7} with quasi-logarithmic step sizes, e.g. a small % increase between integration steps.

[1] Davis: http://arxiv.org/abs/astro-ph/0402278 (2004), Appendix A. All equations converted to Stretch factor S (in place of t and a in Davis).

 

[Jorrie]

Marcus has previously posted many tabular outputs from the TabCosmo calculator, but he had to massage the output considerably in order to make it readable in the

 tags of the editor. The [tex] array option is available, but that requires a lot more manual work - something that the machine could actually do better. I have added an option for a LaTex compatible output and uploaded it as [URL="http://www.einsteins-theory-of-relativity-4engineers.com/TabCosmo7.html"]TabCosmo7[/URL].

It requires you to first play around until you have the range of values that you are interested in, tick the radio button for LaTex, Calculate and then copy and paste the code into a LaTex compatible editor. It is optimized for the PF editor, but you can modify any part of the Tex code after copying (obviously at your own risk :-) 

Please report any problems/suggestions.

Here is a sample output.

[tex]{\scriptsize \begin{array}{|c|c|c|c|c|c|c|}\hline Y_{now} (Gy) & Y_{inf} (Gy) & S_{eq} & H_{0} (Km/s/Mpc) & \Omega_\Lambda & \Omega_m\\ \hline14&16.5&3280&69.86&0.72&0.28\\ \hline\end{array}}[/tex] [tex]{\scriptsize \begin{array}{|r|r|r|r|r|r|r|} \hline S=z+1&a=1/S&T (Gy)&T_{Hub}(Gy)&D (Gly)&D_{then}(Gly)&D_{hor}(Gly)&D_{par}(Gly)\\ \hline1090.000&0.000917&0.000378&0.000637&45.731&0.042&0.056&0.001\\ \hline341.731&0.002926&0.002511&0.003986&44.573&0.130&0.177&0.006\\ \hline107.137&0.009334&0.015296&0.023478&42.386&0.396&0.543&0.040\\ \hline33.589&0.029772&0.089394&0.135218&38.404&1.143&1.614&0.246\\ \hline10.531&0.094961&0.513668&0.772152&31.251&2.968&4.469&1.464\\ \hline3.302&0.302891&2.902232&4.258919&18.588&5.630&10.418&8.506\\ \hline1.035&0.966116&13.274154&13.791148&0.473&0.457&15.728&44.633\\ \hline0.325&3.081570&31.418524&16.391363&-10.476&-32.283&16.428&176.105\\ \hline0.102&9.829121&50.521674&16.496494&-14.143&-139.014&16.496&597.755\\ \hline0.032&31.351430&69.658811&16.499868&-15.295&-479.531&16.500&1942.755\\ \hline0.010&100.000000&88.797170&16.499905&-15.657&-1565.665&16.500&6232.831\\ \hline\end{array}}[/tex]

 

[marcus]

It's a beauty, really is the greatest thing since sliced bread!

I bookmarked http://www.einsteins-theory-of-relativity-4engineers.com/TabCosmo7.html
and will change my signature link.