Coulomb's Law and Electric Fields

[student07]

Examine the charge distribution shown:

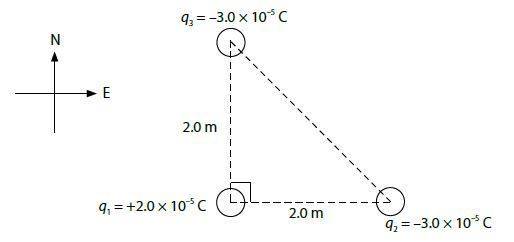
b) What is the net electric field acting on charge 1?

Attempt at the answer:

E2 = Kq2/r2^2 = (9.0 x 10^9 Nm^2/C^2)(3.0 x 10^-5 C) / 2.0m^2

E2 = 6.75 x 10^4 N/C

E2 = E3 ( therefore, same procedure)

eNet = Sqr.rt. 6.75 x 10^4 N/C^2 + 6.75 x 10^4 N/C^2 = 9.55 x 10^4 N/C

angle = Tan^-1 = (6.75/6.75) = 45 deg.

The total electric field acting on charge 1 is 9.55 x 10^4 N/C [N 45deg. E]

Is this right?

 

[nasu]

It looks OK.

 

[student07]

So the reason why charge 1 is not added to the equation is because is the adding of the vectors around it?