- #1
graviton_10
- 5
- 1
- Homework Statement
- A vertical spring mass system is attached in series with another vertical spring mass system. Masses of both objects are different and so are the spring constants of both springs. y1 and y2 are the coordinates measured from the rest position of mass 1 and mass 2 respectively.
I have identified the forces on both masses using free body diagram, but I do not know how to proceed next.
My final goal is to set up matrix equation and then solve for normal frequencies.
- Relevant Equations
- Mq'' = Kq
How should I proceed?
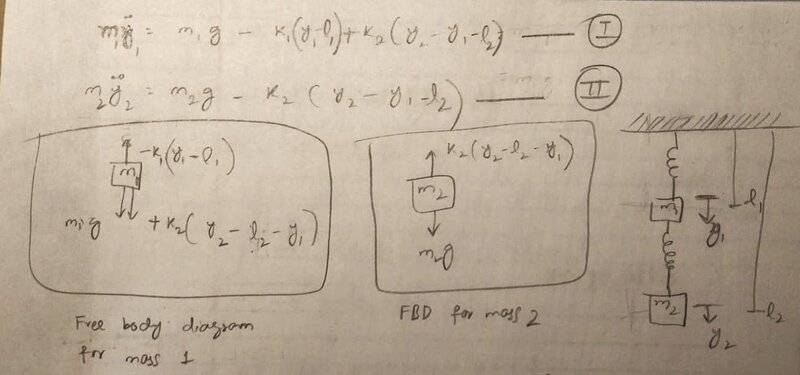
Last edited by a moderator: