Cross product on undivided to components vector

[nhrock3]

he question asks to find the ratio between E0 and B0 and the ratio between w and k
?

E and B are on the x-y plane
they are given as verctors without any components dividing
no x direction part,y direction part,z direction part

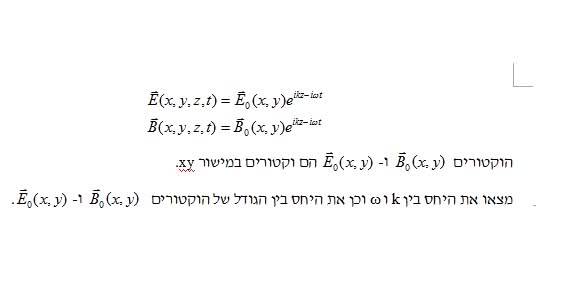
so when when i use the maxwell equations
$$\nabla\times E=-\frac{{dB}}{dt}$$
$$\nabla\times B=\mu_{0}\varepsilon_{0}\frac{dE}{dt}$$

i can't do the cross product of B or E
because i don't know what to put in the tererminant whch is calculating the cross product


i tried to make some components by my self
but i get so many variables

 

[hunt_mat]

In general you can't. You just have yo leave it in the form that you have it. However, there are some things that you can do:
$$\mathbf{E}=\varphi (t,z)\mathbf{E}_{0}(x,y)$$
and likewise for B and there are general rules for this. That is the only way that I can see.

 

[nhrock3]

In general you can't. You just have yo leave it in the form that you have it. However, there are some things that you can do:
$$\mathbf{E}=\varphi (t,z)\mathbf{E}_{0}(x,y)$$
and likewise for B and there are general rules for this. That is the only way that I can see.

what next?

 

[hunt_mat]

So you should have some vector identities which cover it:
so for example:
$$\nabla\times (\varphi\mathbf{E})=\varphi\nabla\times\mathbf{E}+\nabla\varphi\times\mathbf{E}$$
and the like. As I said, there is not much you can do.

 

[nhrock3]

its a very inportant questiom
i don't know what to do next with those identities
could youwrite down how youwould solved it
?

 

[hunt_mat]

$\varphi =e^{ikz-i\omega t}$, so $\nabla\varphi =ike^{ikz-i\omega t}\mathbf{k}$

I will do one of maxwell's equations for you, you can do the rest and we will see where to go from there.
$$\nabla\times\mathbf{E}=-\frac{\partial\mathbf{B}}{\partial t}$$
In our case:
$$\nabla\times\mathbf{E}=e^{ikz-i\omega t}\nabla\times\mathbf{E}_{0}+ik\mathbf{k}\times \mathbf{E}_{0}$$
and also:
$$\frac{\partial\mathbf{B}}{\partial t}=-i\omega \mathbf{B}_{0}e^{ikz-i\omega t}$$
and the equation becomes:
$$\nabla\times\mathbf{E}_{0}+ik\mathbf{k}\times \mathbf{E}_{0}=i\omega\mathbf{B}_{0}$$

 

[nhrock3]

you made a type mistake
iside the formula its E_0
the hole formula is for E

So you should have some vector identities which cover it:
so for example:
$$\nabla\times (\varphi\mathbf{E_0})=\varphi\nabla\times\mathbf{E_0}+\nabla\varphi\times\mathbf{E_0}$$
and the like. As I said, there is not much you can do.

first question:
$$\varphi\nabla\times\mathbf{E_0}$$
means dot product of $$\varphi$$ with $$\nabla\times\mathbf{E_0}$$
but i don't have components of them to do thedot product.
and i don't know how to find
$$\nabla\times\mathbf{E_0}$$


thing that might help is
that the B field and E field are perprendicular(90 degree angle between them)
so there dot product is 0

??

 

[hunt_mat]

Okay, so I edited my previous post to give you an example of what i meant. Can you do this with the other 3 maxwell equations?
The vector identities which you should be aware of are on: http://en.wikipedia.org/wiki/Vector_calculus_identities

 

[nhrock3]

i don't think so
those two are the ones i solved similar question before

how to continue your idea
?

 

[hunt_mat]

By continuing my idea! You saw the sort of thing I did in my post, I gave you a reference for the vector identities. I will do one more only, $\nabla\cdot \mathbf{B}=0$:
$$\nabla\cdot (\mathbf{B}_{0}e^{ikz-i\omega t})=e^{ikz-i\omega t}\nabla\cdot \mathbf{B}_{0}+\mathbf{B}_{0}\cdot\nabla (e^{ikz-i\omega t}) =e^{ikz-i\omega t}\nabla\cdot \mathbf{B}_{0}+ik \mathbf{k}\cdot \mathbf{B}_{0}e^{ikz-i\omega t}$$
Which shows that:
$$\nabla\cdot \mathbf{B}_{0}+ik \mathbf{k}\cdot \mathbf{B}_{0}=0$$

 

[nhrock3]

By continuing my idea! You saw the sort of thing I did in my post, I gave you a reference for the vector identities. I will do one more only, $\nabla\cdot \mathbf{B}=0$:
$$\nabla\cdot (\mathbf{B}_{0}e^{ikz-i\omega t})=e^{ikz-i\omega t}\nabla\cdot \mathbf{B}_{0}+\mathbf{B}_{0}\cdot\nabla (e^{ikz-i\omega t}) =e^{ikz-i\omega t}\nabla\cdot \mathbf{B}_{0}+ik \mathbf{k}\cdot \mathbf{B}_{0}e^{ikz-i\omega t}$$
Which shows that:
$$\nabla\cdot \mathbf{B}_{0}+ik \mathbf{k}\cdot \mathbf{B}_{0}=0$$

ok i wil do gauss law
$$\nabla\cdot (\mathbf{E}_{0}e^{ikz-i\omega t})=\frac{\rho}{\epsilon_0}$$

but still i have to find $$\nabla\cdotE$$
and $$\nabla\cdot B$$
how to do that
?

 

[hunt_mat]

So expand the left hand side, what do you get?

 

[nhrock3]

$$\nabla\cdot (\mathbf{E}_{0}e^{ikz-i\omega t})=\frac{\rho}{\epsilon_0}$$
i wil expand like you did on B

but still i have to find $$\nabla\cdot E_0$$
and $$\nabla\cdot B_0$$
how to do that
?

 

[hunt_mat]

Do you have any sources of charge in your problem? I don't think that you have as you're looking for a wave propagating in the z direction. You still haven't expanded the left hand side of your equation as I did.

Once we have all the reduced equations, ten we will take another look at where we can go from there.

 

[nhrock3]

when you expanded you wrote kk in some place
why didnt you write k^2
?

 

[hunt_mat]

They are different k's. one is a vector direction and the other is effectively a wave number. Keep going.

 

[nhrock3]

it takes me a lot of time to write on latex
so here is a photo of the gauss equaation you said to develop

what is the next step?

 

[hunt_mat]

I think what we're doing here is looking for normal modes and therefore we can set all sources to zero, this will simplify you answer somewhat. You should also be careful about cross products

 

[nhrock3]

ok
but i dint know how to solve it
i followed your lead so far
do you know how to finish it?

 

[hunt_mat]

You have one more to do, Ampere's law, what does that reduce to?

You can't get a ratio of two vectors, so I am not too sure what they're referring to here but I can help you derive a dispersion relation (and equation giving $\omega$ as a function of k.

 

[nhrock3]

not ratio of to vectors but te ratio
of the E0 and B0 coefficient and w ,k coefficient
amperes law uses cross product
which we started from

i followed your lead so far,does it go anyewhere
could you write down the solution to this question
?

 

[hunt_mat]

I am assuming that $\mathbf{E}_{0}$ and $\mathbf{B}_{0}$ are vectors, indeed they have to be.

I will not write down the solution, this website will not give you answers but I will help you find the answer to the problem you're solving.

 

[nhrock3]

no
the exponent is a vector
e^itheta represents a cector with angle
E0 and B0 are coeff

my test is tommorow so i don't have much time please consider this

 

[hunt_mat]

The exponent can't be a vector, it's not possible.

 

[nhrock3]

ok we where doing two equationsthe other two involve cross product
i don't know how to write the cross product term for them

 

[hunt_mat]

The other equation you have is:
$$\nabla\times \mathbf{B}=\frac{1}{\mu_{0}\epsilon_{0}}\frac{ \partial \mathbf{E}}{\partial t}$$
In terms of your assumptions, what does this equation become?

 

[nhrock3]

ok there is no problem to derive by time

how to do the crossproduct?

 

[hunt_mat]

I gave you the link, you have used this method previously and I gave you a link to the vector identities that you will need.