Cubic approximation multivariable taylor series

[abdooo89]

hi everyone , i don't understand these steps for Taylor Expansion , it has used for state space equations
the equations are

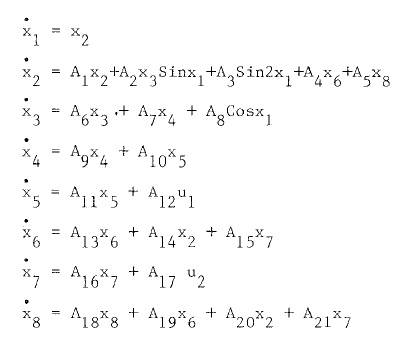
the approximations for sin and cos

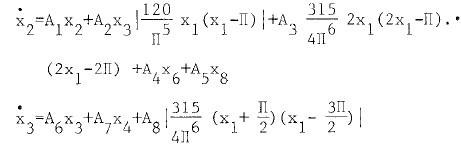
the equation for Taylor series is ( i don't understand at all )

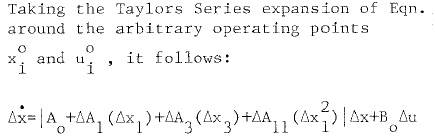
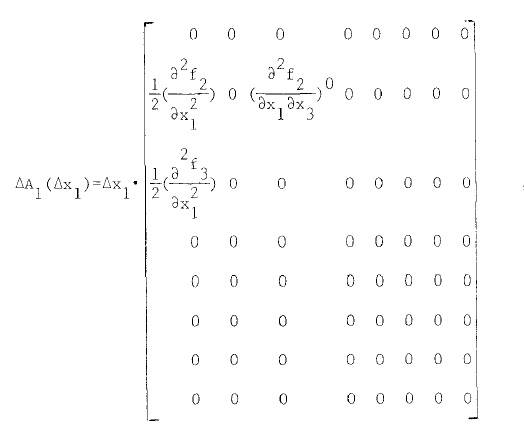
please help me if you can

 

[abdooo89]

please help me

 

[HallsofIvy]

Perhaps people need more help to understand what you are saying. You say "I don't understand these steps for Taylor expansion". The Taylor expansion of what function? And you have "taking the Taylor expansion of Eqn." Of what equation? There seems to be a lot here you are telling us.

 

[abdooo89]

taking the Taylor expansion of Eqn ,

i mean equations ( X'1 to X'8 )

after that Taylor expansion has been taken like that

ΔX'={ A0 + ΔA1(ΔX1)+ΔA3(ΔX3)+ΔA11(ΔX1^2))ΔX+B0 Δu → ( xx)


i don't understand equation ( xx = taylor expansion ) , and how can i get A0 , ΔA1 , ΔA3, ΔA11

i mean which rule they used to get A0 , ΔA1 , ΔA3, ΔA11

the complete file has been attached

 

[Ray Vickson]

taking the Taylor expansion of Eqn ,

i mean equations ( X'1 to X'8 )

after that Taylor expansion has been taken like that

ΔX'={ A0 + ΔA1(ΔX1)+ΔA3(ΔX3)+ΔA11(ΔX1^2))ΔX+B0 Δu → ( xx)


i don't understand equation ( xx = taylor expansion ) , and how can i get A0 , ΔA1 , ΔA3, ΔA11

i mean which rule they used to get A0 , ΔA1 , ΔA3, ΔA11

the complete file has been attached

The author is NOT (at least initially) using Taylor expansions. He uses approximations of the form
$$\sin x_1 \approx p_1(x_1) \equiv \frac{120}{\pi^5} x_1 (x_1 - \pi )\\ \sin 2x_1 \approx p_2(x_1) \equiv \frac{315}{4 \pi^6} (2 x_1 - \pi)(2 x_1 – 2 \pi)\\ \cos x_1 \approx p_3(x_1) \equiv \frac{315}{4 \pi^6} (x_1 + \frac{\pi}{2}) (x_1 - \frac{3 \pi}{2})$$
etcetera. These are not Taylor expansions; if you read carefully you will see that he makes it clear in the article that he claims he is using a form of least-squares approximation to $\sin x_1$, etc. However, it appears the author makes some errors; he should have
$$\sin x_1 \approx \frac{120}{\pi^5} x_1 (\pi - x_1)$$
with sign opposite sign to what he writes; if you plot the two functions you will see that the approximation is not too bad over the interval $x \in [0,\pi]$. However, the approximations $p_2$ and $p_3$ are horrible: they do not resemble the functions $\sin 2x_1$ and $\cos x_1$ at all, as you can see by plotting them.

 

[abdooo89]

First, thank you for your reply, secondly I want to know if this approximations (p2 and p3) are not valid or horrible as you say, what is your advice for me to do?

and why ΔA3 =0

 

[abdooo89]

no one want to help me?