SUMMARY
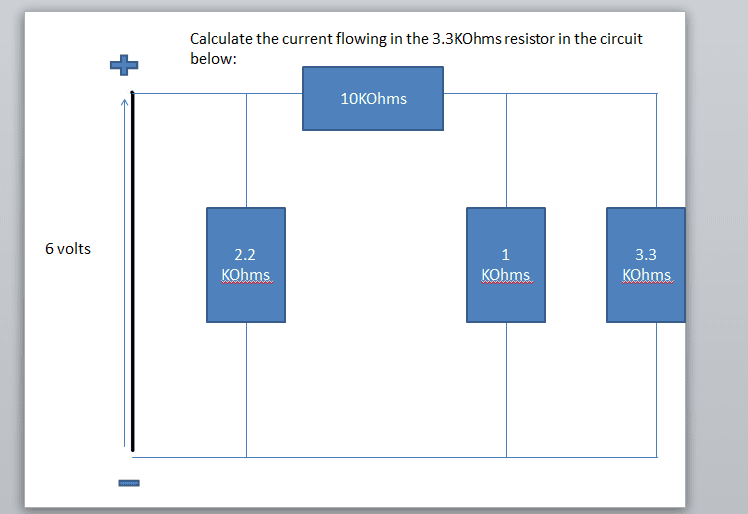
The discussion focuses on calculating current through a resistor network using mesh analysis and Ohm's Law. Participants detail the steps to derive mesh equations for a circuit with resistors of 2.2kΩ, 10kΩ, and a parallel combination of 1kΩ and 3.3kΩ. The final current through the circuit is calculated to be 3.3mA, with specific attention to the application of Kirchhoff's Voltage Law (KVL) and the proper combination of resistors in series and parallel. The importance of maintaining unit consistency throughout calculations is emphasized.
PREREQUISITES
- Understanding of Ohm's Law (V = IR)
- Familiarity with Kirchhoff's Voltage Law (KVL)
- Knowledge of mesh analysis for circuit analysis
- Ability to combine resistors in series and parallel
NEXT STEPS
- Study the application of Kirchhoff's Current Law (KCL) in circuit analysis
- Learn advanced techniques for solving simultaneous equations in circuit analysis
- Explore the Delta-Y transformation for resistor networks
- Practice drawing and analyzing circuit diagrams for complex resistor networks
USEFUL FOR
Electronics students, electrical engineers, and hobbyists seeking to deepen their understanding of circuit analysis and current flow in resistor networks.