- #1
joaofbi1
- 20
- 0
I'm just stuck on a question that I've been given as a quick test, it's really stumped me. I was wondering if anyone could assist me.
Here's the question:
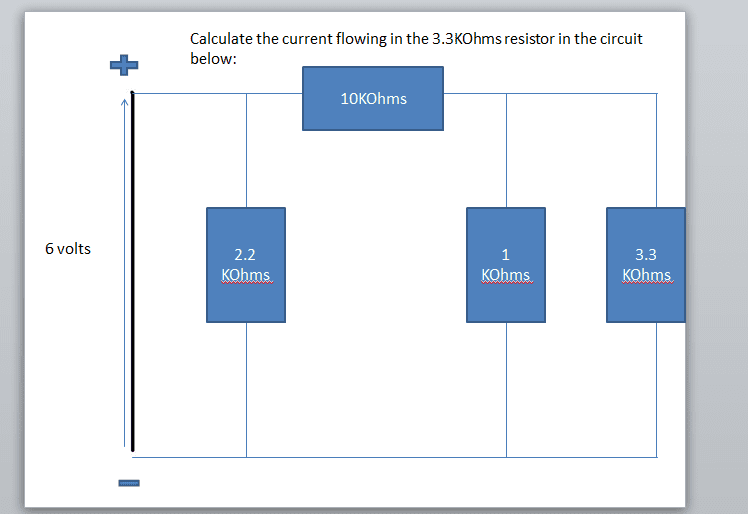
Thank you.
Here's the question:
Thank you.
UltrafastPED said:You can solve this via mesh analysis: write the currents I1,I2,I3 as loops passing around each of the three independent loops, the write the three mesh equations, taking proper care of the directions which you assigned (I used clockwise for all three) when summing the currents from shared resistors.
6V = 2.2k(I1-I2)
0 = 2.2k(I2-I1) + 10k(I2) + 1k(I2-I3)
0 = 1k(I3-I2) + 3.3k(I3)
Then solve the three simultaneous linear equations via your favorite method (substitution, elimination, Cramer's rule), and I3 is your answer.
I also considered a Delta-Y transform but it didn't seem to make the solution go any faster.
NascentOxygen said:I suggested that you should draw some current paths, to help with the analysis, for a good reason.
Keep it as 3 resistors, 2.2, 10 and 0.8. Draw some current paths, these being shown as closed loops.
UltrafastPED said:The 10k and 0.8k resistors are in series; the 2.2k is NOT in parallel with the 0.8k resistor because there is something on the upper bus between them: the 10k resistor.
So combine the 10k with the 0.8k in series: 10.8k, and then you are left with two resistors in parallel, the 2.2k and the 10.8k. Combine them and then solve for the total current.
Not exactly.joaofbi1 said:So once I get the current for the 10.8 resistor do I divide that current by 1and 3.3
How many volts are lost across the 10k resistor? Use Ohms Law.joaofbi1 said:Im quite confused, what calculations would I need to perform?
UltrafastPED said:It should be 3.3 mA through 10k ohms. Pay attention to your units!
And that is the total current; we previously calculated the current for this branch - what is it?
joaofbi1 said:So how do I Calculate how much mA I have lost through the resistor?
I2 = 6 V/10.8 k ohms = 0.55 mA