SUMMARY
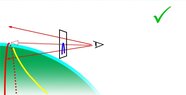
The forum discussion centers on the calculation of the visible curvature of the horizon from various altitudes, with the author seeking publication advice for their paper on this topic. Key points include the angular depression of the horizon, which increases with altitude and can be measured using a theodolite. The discussion also touches on the mathematical treatment of horizon curvature, emphasizing the visual perception of the horizon as altitude increases. The author clarifies that their work focuses on graphing the horizon's curvature as seen by an observer, distinguishing it from basic distance calculations.
PREREQUISITES
- Understanding of angular depression and its measurement using a theodolite.
- Familiarity with basic trigonometry and its application to curvature calculations.
- Knowledge of spherical geometry and the concept of horizon curvature.
- Awareness of scientific publication processes and literature review practices.
NEXT STEPS
- Research the impact of altitude on horizon curvature using mathematical models.
- Explore journals that publish papers on observational astronomy and geodesy.
- Learn about the effects of atmospheric refraction on horizon visibility.
- Investigate the differences between spherical and oblate spheroid models in horizon calculations.
USEFUL FOR
This discussion is beneficial for researchers, mathematicians, and educators interested in the visual and mathematical aspects of horizon curvature, as well as those looking to publish scientific papers in related fields.