SUMMARY
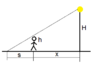
The discussion focuses on calculating the rate at which a man's shadow decreases as he walks towards a lamp. The man is 6 feet tall and moves at a velocity of 5 feet per second towards a lamp positioned 15 feet above the ground. To solve this problem, participants suggest using dynamic equations and establishing a relationship between the man's position and the length of his shadow through geometric principles.
PREREQUISITES
- Understanding of similar triangles in geometry
- Basic knowledge of calculus, specifically related rates
- Familiarity with dynamic equations
- Ability to create and interpret geometric diagrams
NEXT STEPS
- Study the concept of related rates in calculus
- Learn how to set up and solve problems involving similar triangles
- Explore dynamic equations and their applications in physics
- Practice drawing geometric diagrams to visualize problems
USEFUL FOR
Students studying calculus, particularly those focusing on related rates, as well as educators looking for practical examples of geometric applications in real-world scenarios.