Defining a vector in magnitude,angle form.

[Hijaz Aslam]

I've learned that vectors can be defined in,basically, two ways. (1) Unit Vector Form (xi+yj+zk) (2)Magnitude angle form.
The second form always adds a confusion in problems. For instance let's define a function A and B as:

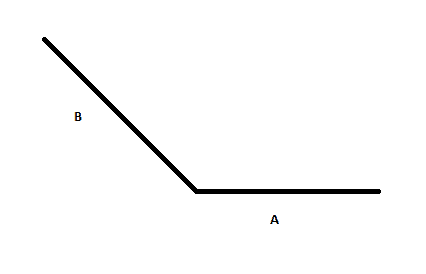
When we define -B why do we do it as follows:

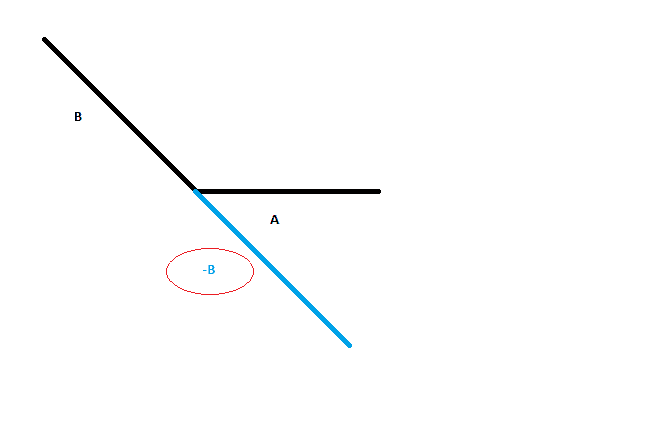
I mean why do we write it as -B isn't the information of the direction clear from the angle between A and the Blue line?

 

[SteamKing]

You may not always have a diagram to refer to, especially if your vector calculations get long and involved.