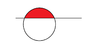
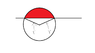
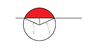
The discussion revolves around determining the domain for the polar coordinate function f(x,y) = y(x² + y²)⁻¹, with constraints y ≥ 1/2 and x² + y² ≤ 1. Participants clarify the limits for r and θ, emphasizing that the lower limit for r depends on the angle θ, particularly when intersecting the line y = 1/2. There is confusion about the correct values for these limits, with a consensus that the upper limit for r is 1 and the lower limit varies based on θ. The conversation highlights the importance of visualizing the region and understanding how the polar coordinates relate to the Cartesian constraints. Ultimately, the participants arrive at a clearer understanding of how to express the limits for r in relation to θ.