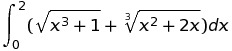SUMMARY
The integral of the square root and cube root presented in the discussion is confirmed to yield a result of 6, as verified by WolframAlpha. The user initially attempted to solve the integral using substitution but encountered difficulties. It is established that this integral cannot be solved using elementary functions. Instead, the discussion suggests applying the formula for the integral of the square root of a sum of squares, specifically $$\int\sqrt {x^2+a^2}dx=\frac{x\sqrt {x^2+a^2}}{2}+\frac{a^2}{2}ln(x+\sqrt {x^2+a^2})$$ for further progress.
PREREQUISITES
- Understanding of integral calculus
- Familiarity with substitution methods in integration
- Knowledge of logarithmic functions
- Ability to apply specific integral formulas
NEXT STEPS
- Study the application of the integral formula for $$\int\sqrt {x^2+a^2}dx$$
- Explore advanced integration techniques beyond elementary functions
- Learn about the use of computational tools like WolframAlpha for integral verification
- Investigate the properties of logarithmic functions in calculus
USEFUL FOR
Students and educators in mathematics, particularly those focused on calculus and integral techniques, as well as anyone interested in advanced integration methods.