Density of balls submerged in a liquid and connected by a hard rod

[Combinatorics]

Homework Statement

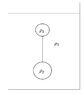
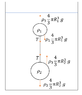
Given the following system (see the attached image) of two balls connected by a thin rod with negligible mass. The upper ball has a radius $R_1$ and density $\rho_1$ and the lower ball has a radius $R_2$ and density $\rho_2$. This system is submerged in a liquid with density $\rho_3$, where it floats in a stable equilibrium as shown in the image I attach.
Show that $\rho_2>\rho_1$, and $\rho_3 = \frac{\rho_1 R_1^3 + \rho_2R_2^3 }{R_1^3 + R_2 ^3 }$.

Relevant Equations

Bernoulli equation $p+\rho gH+ 0.5 \rho v^2 = \text{constant}$
Buoyancy force $B = \rho_3 V g$

Performing force balance on the two balls, I obtain
$T+\frac{4\pi}{3}g \rho_3 R_1 ^3 = \frac{4\pi}{3}g \rho_1 R_1^3$
$T+\frac{4\pi}{3}g \rho_2 R_2^3 = \frac{4\pi}{3}g \rho_3 R_2^3$
from which I obtain $\rho_3 = \frac{\rho_1 R_1^3 + \rho_2R_2^3 }{R_1^3 + R_2 ^3 }$ and $2T =\frac{4\pi}{3}g\rho_1R_1^3 - \frac{4\pi}{3}g \rho_2 R_2^3$.
Unfortunately, I have no idea how can I find any information regarding $\rho_1,\rho_2$. I thought Bernoulli equation might help here, since the different pressures experienced by the two balls play a role here, but I do not know how to do it (as far as I know, Bernoulli equation may not be applicable in such a case, where there is more than just one liquid involved).

Will be happy to receive some help here. Thanks!

 

[rsk]

The 2nd bit you can get by considering the object as a whole - ie the total downards force (total weight) must be equal in magnitiude to the total upwards force (total upthrust).

For the first bit, you need your 2nd diagram. Consider the forces acting on one sphere at a time. Since the T is acting in opposite directions on each, you can compare the U and W of each and hence the density of each against the density of the liquid.

 

[Combinatorics]

The 2nd bit you can get by considering the object as a whole - ie the total downards force (total weight) must be equal in magnitiude to the total upwards force (total upthrust).

For the first bit, you need your 2nd diagram. Consider the forces acting on on sphere at a time. Since the T is acting in opposite directions on each, you can compare the U and W of each and hence the density of each against the density of the liquid.

Hi rsk, I am not sure if I understand you correctly. Do you mean that I should use that
$\frac{4\pi}{3}g \rho_1 R_1^3= T+\frac{4\pi}{3}g \rho_3 R_1 ^3$
$\frac{4\pi}{3}g \rho_2 R_2^3 = \frac{4\pi}{3}g \rho_3 R_2^3 - T$
?
If so, then how can I say something about the relationship between $\rho_1$ and $\rho_2$ without any information on the radiuses $R_1,R_2$?

Thank you!

 

[rsk]

Look at your first equation. You have two terms which contain 4/3 pi g R² but they have different values for density. So, if the ball is in equilibrium, is rho 1 bigger or smaller than rho 3?

Do the same with your 2nd equation and you should now be able to compare rho1 and rho2

 

[Lnewqban]

...
Unfortunately, I have no idea how can I find any information regarding $\rho_1,\rho_2$. I thought Bernoulli equation might help here, since the different pressures experienced by the two balls play a role here, but I do not know how to do it (as far as I know, Bernoulli equation may not be applicable in such a case, where there is more than just one liquid involved).

Will be happy to receive some help here. Thanks!

I would use the concept of static rotational stability of the whole floating body (m1-thin rod-m2) to try to solve question #1.

Please, see:
https://en.m.wikipedia.org/wiki/Buoyancy#Static_stability

Let's assume for a moment that $R_1=R_2$.
If ball #2 is heavier than ball #1, the center of gravity of the system is located below the center of bouyancy (both balls displace the same volume of fluid; therefore, this center should be located midway).

Would that idea work for $R_1≠R_2$?

 

[rsk]

I would use the concept of static rotational stability of the whole floating body (m1-thin rod-m2) to try to solve question #1.

Please, see:
https://en.m.wikipedia.org/wiki/Buoyancy#Static_stability

Let's assume for a moment that $R_1=R_2$.
If ball #2 is heavier than ball #1, the center of gravity of the system is located below the center of bouyancy (both balls displace the same volume of fluid; therefore, this center should be located midway).

Would that idea work for $R_1≠R_2$?

You don't need anything as complicated as that, the question is simpler than it first appears

 

[haruspex]

Hi rsk, I am not sure if I understand you correctly. Do you mean that I should use that
$\frac{4\pi}{3}g \rho_1 R_1^3= T+\frac{4\pi}{3}g \rho_3 R_1 ^3$
$\frac{4\pi}{3}g \rho_2 R_2^3 = \frac{4\pi}{3}g \rho_3 R_2^3 - T$
?
If so, then how can I say something about the relationship between $\rho_1$ and $\rho_2$ without any information on the radiuses $R_1,R_2$?

Thank you!

It's a stability question, so you need to think about what would happen if they were not arranged vertically. Suppose they were placed in the fluid with the bar horizontal. What wouid happen, and in terms of forces, why?

 

[rsk]

It's a stability question, so you need to think about what would happen if they were not arranged vertically. Suppose they were placed in the fluid with the bar horizontal. What wouid happen, and in terms of forces, why?

Again, it's not that complicated. Just free body force diagrams. For the first part for the balls individually, for the 2nd part for the whole thing.

 

[etotheipi]

For complete proof of stability you must check that body performs SHM when subjected to small perturbation. Notice that the torque on the configuration about the centre of mass is$$\tau = \frac{16 \pi^2 R_1^3 R_2^3 g l}{9(m_1 + m_2)} \left[ \rho_2(\rho_1 - \rho_3) + \rho_1(\rho_3 -\rho_2) \right] \sin{\theta}$$Since the leading coefficient is strictly positive, SHM is only achieved for small angular perturbation in $\theta$ if $\left[ \rho_2(\rho_1 - \rho_3) + \rho_1(\rho_3 -\rho_2) \right] = (\rho_1 - \rho_2) \rho_3 < 0$. Or in other words, if $\rho_2 > \rho_1$.

 

[rsk]

For complete proof of stability you must check that body performs SHM when subjected to small perturbation. Notice that the torque on the configuration about the centre of mass is$$\tau = \frac{16 \pi^2 R_1^3 R_2^3 g l}{9(m_1 + m_2)} \left[ \rho_2(\rho_1 - \rho_3) + \rho_1(\rho_3 -\rho_2) \right] \sin{\theta}$$Since the leading coefficient is strictly positive, SHM is only achieved for small angular perturbation in $\theta$ if $\left[ \rho_2(\rho_1 - \rho_3) + \rho_1(\rho_3 -\rho_2) \right] = (\rho_1 - \rho_2) \rho_3 < 0$. Or in other words, if $\rho_2 > \rho_1$.

Not necessary.

 

[etotheipi]

Not necessary.

Well, you must show that system is stable to small perturbations, either by writing down the equations of motion, or otherwise by defining the effective potential energy of the system [e.g. by integrating my expression for torque] and showing that the system is at a local minimum. Both, are equivalent ways of saying the same thing.

I don't believe, there is another way that is rigorous. But, I could be mistaken. What did you have in mind?

 

[rsk]

I didn't want to do this, as I thought the original poster might want to do it himself. However, since there are people here who are determined to make it as complex as possible, here goes.

Combinatorics STOP READING HERE IF YOU WANT TO DO IT YOURSELF FIRST!

For part 1
Consider first ball 1 and the forces on it, weight W, upthrust U and tension T.

For equilibirum we have U = W + T this U > W and so rho3 > rho1

Similarly for ball 2 W = U + T so W > U so rho2 > rho 1

Therefore by logic rho2 > rho1For part 2
The weight of the whole thing is 4/3 pi g (R1 ³ x rho1 + R2³ rho2) and the upthrust is 4/3 pi g (R1³ + R2³) rho3

Since W = U we equate these, rearrange and Voila!

Really, physics is meant to be simple and elegant. Don't overegg the pudding.

 

[rsk]

Well, you must show that system is stable to small perturbations,

No, you are not asked to show that. You are told that is the case.

 

[haruspex]

Again, it's not that complicated. Just free body force diagrams. For the first part for the balls individually, for the 2nd part for the whole thing.

I don't see how what I suggested differs from your solution in post #12.

 

[etotheipi]

For part 1
Consider first ball 1 and the forces on it, weight W, upthrust U and tension T.
For equilibirum we have U = W + T this U > W and so rho3 > rho1
Similarly for ball 2 W = U + T so W > U so rho2 > rho 1
Therefore by logic rho2 > rho1

The stress in the rod is not constrained to be tensile; it could be compressive. That is, you cannot assume a priori that $T > 0$. I maintain that, a rigorous analysis requires analysis of behaviour of the system under small perturbation.

 

[rsk]

It's a stability question, so you need to think about what would happen if they were not arranged vertically. Suppose they were placed in the fluid with the bar horizontal. What wouid happen, and in terms of forces, why?

I don't see how what I suggested differs from your solution in post #12.

I note the words "upper" and "lower" in the question and realize that they cannot therefore be horizontal.

 

[rsk]

The stress in the rod is not constrained to be tensile; it could be compressive. That is, you cannot assume a priori that $T > 0$. I maintain that, a rigorous analysis requires analysis of behaviour of the system under small perturbation.

If the stress in the rod is compressive, which ball is heaviest? Can it then be considered to be "in stable equilibrium" as stated in the question?

 

[etotheipi]

If the stress in the rod is compressive, which ball is heaviest? Can it then be considered to be "in stable equilibrium" as stated in the question?

That's why I said "a priori". And indeed, you find that it cannot be compressive in stable equilibrium! But to show that rigorously, i.e. by not just appealing to intuition, you must perform the perturbation analysis!

In other words, your argument only holds so long as we already verified the arrangement with the heavier mass on the bottom is the stable arrangement. I.e. it does not add anything that we already do not know!

 

[haruspex]

I note the words "upper" and "lower" in the question and realize that they cannot therefore be horizontal.

You misunderstand. That was a thought experiment to help @Combinatorics see what would happen if it were only slightly displaced from the vertical.
Providing hints this way is preferable to posting full solutions until the OP has had a chance to make use of them. Beyond that, considering extreme cases is a useful technique for students to practise.

 

[Combinatorics]

Look at your first equation. You have two terms which contain 4/3 pi g R² but they have different values for density. So, if the ball is in equilibrium, is rho 1 bigger or smaller than rho 3?

Do the same with your 2nd equation and you should now be able to compare rho1 and rho2

Thank you! I completely missed this small step.

I would use the concept of static rotational stability of the whole floating body (m1-thin rod-m2) to try to solve question #1.

Please, see:
https://en.m.wikipedia.org/wiki/Buoyancy#Static_stability

Let's assume for a moment that $R_1=R_2$.
If ball #2 is heavier than ball #1, the center of gravity of the system is located below the center of bouyancy (both balls displace the same volume of fluid; therefore, this center should be located midway).

Would that idea work for $R_1≠R_2$?

Thank you! It was interesting to read.

 

[Lnewqban]

...
Thank you! It was interesting to read.

You are welcome
As you can see, Bernoulli could not help you in this case because there is no velocity (your system is not moving), or any substantial pressure differential due to limited depth of your system within the fluid.