Deravatives help(I think it's done by chain rule)

[Goethe10]

Hi everybody I'm trying to solve this equation
the text in shown picture basically asks to find meaning of Xo

By doing this

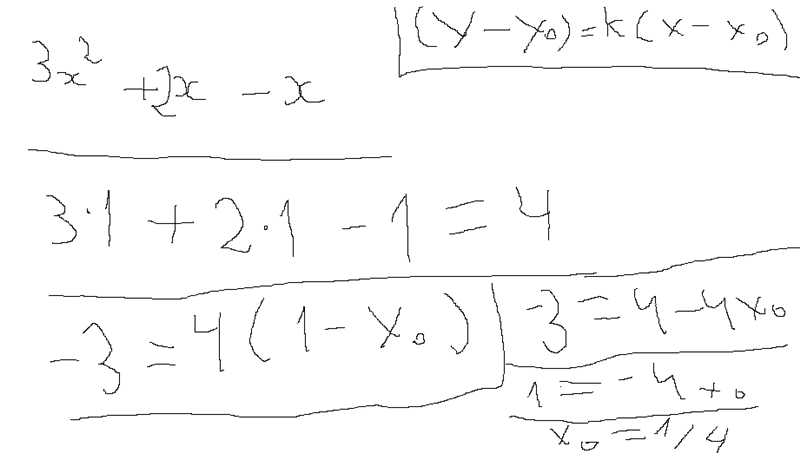
But it says my answer is wrong, can anyone tell me why, Thank you?(Also what is this equation called in English?)

 

[HallsofIvy]

You title this "derivatives help", but then say "I am trying to solve this equation". But then you do NOT give any equation, rather a function $f(x)= x^3+ x^2- 2x+ 3$.

I think you are trying to find the equation of the tangent line at (1, -3). You have below that $3x^2+ 2x- x$ but don't say what that is! I think you meant to find the derivative but, if so, it is wrong. "$3x^2$" is the derivative of $x^3$, "$2x$" is the derivative of $x^2$ and "0" is the derivative of the constant -3, but the derivative of "$-2x$" is -2, NOT x.
The derivative is $3x^2+ 2x- 2$. Evaluate that at x= 1 to find the slope of the tangent line.

You have the formula "$y- y_0= m(x- x_0)$" up on the right side. That is, of course, the equation of a line through the point $(x_0, y_0)$ with slope m. But you don't use that or write the equation of the tangent line in that form. I see "$-3= 4(1- x_0)$". In addition to the incorrect slope (4 is wrong), you have x and $x_0$ reversed. "$x_0$" is the "1" of (1, -3).

And, no, the "chain rule" has nothing to do with this.

 

[micromass]

Can you please translate this:

 

[Goethe10]

I figured it out :P
Thanks Ivy.
@Micromass
I can't unfortunately. well Here is what I did
I found derivative of f(x)= x^3+x^2-2x-3
which is 3x^2+2x-2
I knew that X0=1 and Y0=-3
then I inserted 1 instead of X0 and got 3
So I used this formula
(Y-y0)=K(x-x0)
I inserted x0 and y0 and I got
Y + 3 = 3( X - 1)
I made Y=0, since I want to find Abscissa(x0)
So 3 = 3x - 3
6 = 3x
x = 2.