Derivation of Rutherford Scattering - angular momentum

[alexjean]

Homework Statement

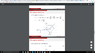
I am trying to show that as the alpha particle is being scattered, the angular momentum magnitude at point M is $m r^2 \frac{d \phi}{dt}$.

Diagram:

Homework Equations

Linear Momentum: $\vec L = \vec r \times \vec p$
Repulsive Coulomb Force: $\vec F = \frac{k 2Ze^2}{r^2} \frac{\vec r}{r}$

The Attempt at a Solution

As the alpha particle approaches the nucleus, the repulsive force begins acting on it. Changing it's velocity:
$\vec v_M = \int_{t_{-\infty}}^{t_{M}} \frac{\vec F(\phi)}{m} t \, dt + \vec v_0$

If I could solve that integral, I would know the velocity for any angle $\phi$. Allowing me to solve for angular momentum in terms of $\vec r$. However, that integral is a mess. I would need to get time, $t$ in terms of $\phi$. I've attempted that below, but it doesn't look promising:

$t = \frac{\Delta \vec r}{\vec v}$
$t = \int \frac{1}{\vec v} \, d\vec r$,
$t_M = \int_{<-\infty,0>}^{\vec r_M} \frac{1}{\vec v} \, d\vec r$
$\frac{dt}{d\vec r} = \frac{1}{\vec v}$

Substituting into the original integral:
$\vec v_M = \int_{<-\infty,0>}^{\vec r_M} \frac{\vec F(\phi)}{m} (\int_{<-\infty,0>}^{\vec r_M} \frac{1}{\vec v} \, d\vec r) \frac{1}{\vec v} \, d\vec r + \vec v_0$

Most derivations of this I've found online seem to glaze over the determination of angular momentum at point M, making me think I've missed something simple. Could anyone point me toward a better approach?

 

[ehild]

Homework Statement

I am trying to show that as the alpha particle is being scattered, the angular momentum magnitude at point M is $m r^2 \frac{d \phi}{dt}$.

Diagram:
View attachment 94534

Homework Equations

Linear Momentum: $\vec L = \vec r \times \vec p$
Repulsive Coulomb Force: $\vec F = \frac{k 2Ze^2}{r^2} \frac{\vec r}{r}$

The Attempt at a Solution

As the alpha particle approaches the nucleus, the repulsive force begins acting on it. Changing it's velocity:
$\vec v_M = \int_{t_{-\infty}}^{t_{M}} \frac{\vec F(\phi)}{m} t \, dt + \vec v_0$

The angular momentum is $L=\vec L = \vec r \times \vec p$.
Is M the point of closest approach?
The momentum ,##vec p = m \vec v. In polar system of coordinates, the velocity has a radial component and a transversal one. See http://pioneer.netserv.chula.ac.th/~anopdana/211/24rtheta.pdf The vector product with the radial component is zero. The transversal component of the velocity is r dφ/dt. It is easy to get angular momentum from here.