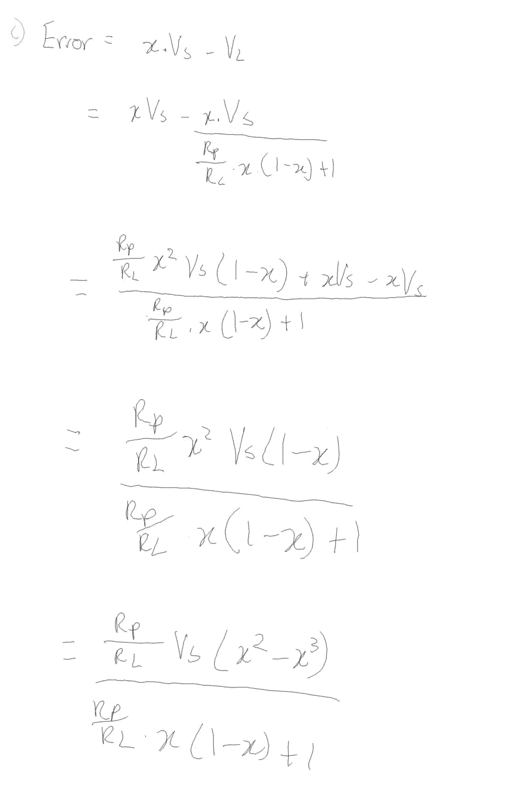berkeman said:
Sorry, I'm not able to decode your equations at all. Others may be able to, though.
It always helps to start with a schematic or figure, to be sure everybody understands the terminology and the variables. For example, I have no idea what you mean by:
And I'm not able to understand your use of parenthesis. I think that I finally figured out that "." means multiplication, but I'm not even sure about that.
In general, it's best if you learn to use basic LaTeX for writing math equations online. We have a tutorial on that under INFO, Help at the top of the page.
In any case, I would think the error would be the difference in the wiper voltage between having the load resistor connected or not, right?
https://upload.wikimedia.org/wikipe...oad.svg/474px-Potentiometer_with_load.svg.png
View attachment 260259
If RL is infinite, then you just get the voltage divider between R1 and R2. If RL is finite, that modifies the voltage divider equation. Is that what you were trying to do with your work?
Hi, thanks for your reply! I didn't know LaTeX was an option for writing equations on here. I've re-done them below. I thought "." was a common convention for multiply, but maybe that's just in Europe. Sorry about the confusion. I've used "*" this time around for the multiply symbol.
The diagram you attached is correct and I think we are on the same page. Essentially, I am looking to calculate the error from having R
L as infinite and finite.
In the case of my workings, R_1 = (1-x)*R_p\ and\ R_2 = x*R_p
where x is the fraction of the resitor the wiper is at.
From this:
V_{out} =\frac{V_s}{R_{total}} * R_{out}
R_{out} = x * R_p || R_L
R_{out} = \frac{x*R_p*R_L}{x*R_p + R_L}
R_{total} = (1-x)*R_p + R_{out}
R_{total} = (1-x)*R_p + \frac{x*R_p*R_L}{x*R_p + R_L}
=> V_{out} = \frac{V_s}{(1-x)*R_p + \frac{x*R_p*R_L}{x*R_p + R_L}} * \frac{x*R_p*R_L}{x*R_p + R_L}
V_{out} = \frac{V_s*x}{\frac{R_p}{R_L}*(1-x) + 1}
With an infinite R
L, \frac{R_p}{R_L} = 0 => V_{out} = V_s * x
With a finite R
L, it can't be simplified
Following from this, the error is then
x*Vs - \frac{V_s*x}{\frac{R_p}{R_L}*(1-x) + 1}
Which I then break down in my workings from the previous post to :
\frac{ \frac{R_p}{R_L} * V_s * (x^2-x^3)}{\frac{R_p}{R_L}*(1-x) + 1}
However, in my lecture slides and textbooks, the correct result for error is:
\frac{Rp}{RL} * V_s * (x^2-x^3)
I don't see the step in between my final line of workings and that? I assume I am missing something else? Thanks